Research on High-precision Blackbody Temperature Control Based on Priority Fusion Algorithm
-
摘要:
为优化红外成像光谱仪探测性能，提出了一种具有用户自定义指标和温控精度达到1.0 mK的优先级融合控制算法（Priority fusion algorithm，PFA），该算法将基础PID、模糊PID和自抗扰控制算法与BP神经网络算法相融合，能够实现高性能黑体温控。通过Simulink仿真实验，仿真结果表明，与传统算法相比，PFA算法的超调量从3.606%下降到0.101%，响应时间从64 min下降到14.4 min，温度控制精度达到1.0 mK。同时搭建了黑体辐射定标平台，物理实验结果与理论模拟结果基本一致。该模型为高精度温控黑体在空间遥感领域的实际应用奠定理论基础，在温控领域具有重大意义。
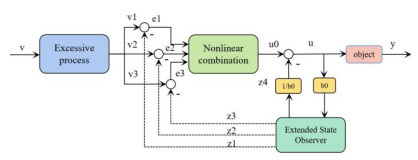
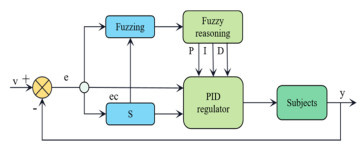
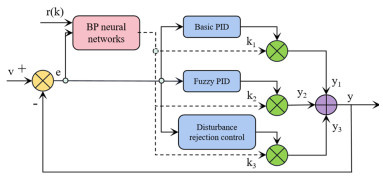
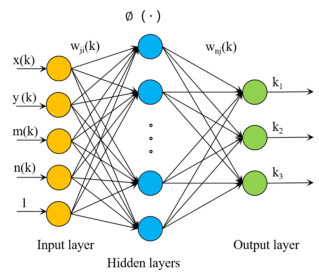
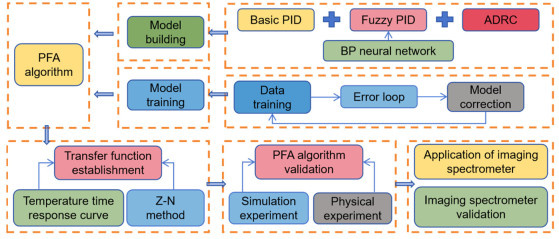
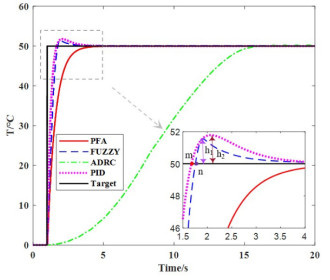
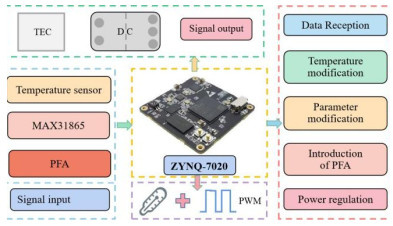
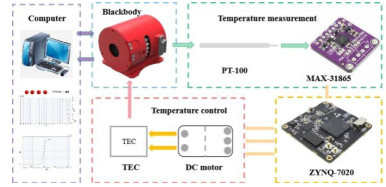
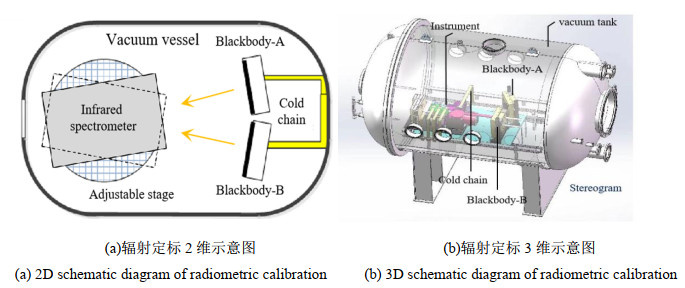
Abstract:To optimize the detection performance of infrared imaging spectrometers, a priority fusion temperature control algorithm (PFA) with user-defined indicators and a temperature control accuracy of 1.0 mK is proposed. This algorithm combines basic proportional–integral–derivative (PID), fuzzy PID, and self-disturbance rejection control algorithms with the BP neural network algorithm to achieve high-performance blackbody temperature control. Results of Simulink simulation experiments show that compared with traditional algorithms, the overshoot of the PFA algorithm decreases from 3.606% to 0.101%, the response time decreases from 64 min to 14.4 min, and the temperature control accuracy reaches 1.0 mK. Simultaneously, a blackbody radiation calibration platform is built, and the physical experimental results are consistent with the theoretical simulation results. This model lays the theoretical foundation for the practical application of the high-precision temperature controlled blackbody in the field of space remote sensing and has remarkable significance in the field of temperature control.
-
0. 引言
随着长波红外探测器技术的成熟，无论民品还是军品市场对于长波红外镜头的需求日益增长，尤其在车载无热化镜头，导引头用红外镜头等领域，而这些产品对镜头的成像质量、环境适应性、成本均有比较苛刻的要求。
比利时的Schuster N分别利用机械被动式、光学被动式和光学机械混合被动无热化方式，实现两片透镜系统－40℃~80℃的无热化设计，其焦距50 mm，F/1.3，波段8~13 μm。通过对比，他们证实利用光学机械混合被动无热化，可有效降低红外镜头无热化的成本[1]。
国内对于无热化镜头的研究主要集中在折衍混合消热差和硫系玻璃的运用上[2-4]。哈尔滨工业大学的关英姿等人对比了光学被动无热化和机械被动无热化的特点，指出无热化方案的选取应综合考虑性能、尺寸、重量、成本等方面的要求[5]。华北光电技术研究所杨加强等人，实现焦距25 mm，F/1的三片式无热化镜头设计加工[6]。镜筒材料选用铝，光学系统采用折衍混合的光学被动无热化方法，包含4个非球面和1个衍射面，总长32 mm。
所谓混合无热化即采用两种或两种以上的无热化方式，例如王学新等人研究了光学被动式和机电式组合消热差方法[7]。混合无热化的主要目的是克服单一无热化方式实现困难或需要较高投入的问题，以实现低成本、高性能的无热化效果。
1. 设计要求及思路
某导引头用长波红外无热化镜头的设计指标如表 1所示。其焦距要求较长，且探测器像元尺寸较小，需要光学镜头提供足够的能量，确定其F数为1。为满足弹载使用环境，要求体积重量尽可能小，且满足－40℃~60℃被动无热化。
表 1 设计指标要求Table 1. Requirements of design parametersParameters Value Focal length 75 mm Wavelength 8μm~12 μm Temperature －40℃~+60℃ F/# 1 Field of view 5.86°×4.69° MTF@42 lp/mm On axis＞0.4 Out axis＞0.3 Detector 640×512，12 μm 被动无热化分为光学被动式和机械被动式。光学被动式是选用不同的光学和结构材料，通过合理分配光焦度，加入衍射元件等方式实现消热差。机械被动式通常是利用不同膨胀系数的结构材料，在不同温度下通过结构设计驱动镜头整体或部分透镜轴向运动以补偿热离焦。光学被动式需要较为复杂的光学结构，设计难度大，限制因素多，但是其无热化效果较好。机械被动式成本较低，但是要利用多层镜筒结构，体积重量偏大，无热化效果也难以保证[8-10]。
本文所提的混合被动无热化方法是利用光学被动热化选用合适的材料和光焦度分配，实现单个透镜轴向微量移动以补偿热差，再利用较少的热补偿材料通过简单的结构形式驱动透镜按要求移动，以实现低成本、高性能的无热化效果。
2. 不同被动无热化光学设计对比
2.1 光学被动无热化
光学被动无热化设计时，承担主要光焦度的透镜，一般选用折射率温度系数较小的材料，并且通过加入衍射元件以进一步减小系统热差。针对表 1的指标要求，通过多轮优化，最终确定“硫系-锗-硒化锌”的光学被动无热化结构，如图 1所示。该系统3块透镜各有一个非球面，其中有一面为非球面与衍射面的结合。光学系统设计总长80 mm，总重257 g，全视场畸变小于等于0.7%。
图 2为－40℃、20℃、60℃时，特征频率42 lp/mm处不同视场调制传递函数MTF（modulation transfer function），可以看出不同温度下各视场成像质量满足技术要求。
利用光学设计软件进行公差分析。采用CODE V默认公差，像面移动为补偿器，结果显示中心视场MTF@42 lp/mm从设计值0.42降低到0.36的概率约为98%，其他视场考虑公差后MTF均大于等于0.26（概率98%）。常规加工装调精度即可满足系统要求。
2.2 混合被动无热化
混合被动无热化的主要目的是减小光学被动无热化的设计、加工难度，同时减小机械被动无热化的结构复杂度。为此，尽可能简化光学系统省去衍射面，减小加工难度；选取容易驱动，且对镜头整体外形包络影响较小的透镜作为热差补偿元件。
参考光学被动无热化结构形式，省去衍射面，并对光学材料进行调整，优化后选用“硫系-硫化锌-锗”的结构形式，如图 3所示。该系统每块透镜各有一个非球面，设计总长75 mm，总重248 g，全视场畸变小于等于1.3%。
图 4为－40℃、20℃、60℃下特征频率42 lp/mm处不同视场调制传递函数，可以看出不同温度下系统成像质量与光学被动无热化相当。
如图 3所示，透镜1和透镜2口径相对较大，如果选作热差补偿元件，在其径向设置机械被动调节机构会增大系统的体积、重量；而选择透镜3作为热差补偿元件，则可以有效减小调节机构的体积和重量，从而有利于系统的小型化、轻量化。因此，选择透镜3作为热差补偿元件。透镜3轴向移动以适应不同环境温度。为了减小透镜3的位移，利用多重结构兼顾各个温度下的成像质量和透镜3的移动量，使其尽可能小。如表 2所示，低温时透镜3向透镜2移动，为负值；高温时则反方向运动。
表 2 不同温度下透镜3的相对位移Table 2. Shift of the lens 3 under different temperatureTemperature /℃ －40 20 60 Displacement/mm －0.052 0 0.034 与光学被动无热化设计相同，采用CODE V默认公差，对系统进行公差分析，结果显示中心视场MTF@42 lp/mm以98%的概率，从设计值0.46降到0.36。反转灵敏度分析显示，该系统透镜1中心厚和中心偏公差比光学被动无热化系统稍严。但是，总体来说两种设计公差要求相当，常规加工装调精度均可满足要求。
3. 混合被动无热化结构设计
混合被动无热化只需简单的多层镜筒结构，驱动单个透镜移动即可。对所设计的混合被动无热化光学系统进行结构设计，如图 5所示。镜筒、隔圈、压圈等材料选用铝合金，选用线膨胀系数较大的聚甲醛（POM, polyformaldehyde）作为热补偿材料。设计3层镜筒结构，中间层为POM，其前后两端分别与外层、内层镜筒粘接。温度变化则POM热胀冷缩，能够驱动透镜3按照设计所需的规律移动。
![]()
图 5 混合被动无热化结构示意图Figure 5. Mechanical schematic diagram of hybrid passive athermalization为了保证不同温差ΔT，透镜3的相对移动量ΔL满足光学设计要求，POM的长度Lpom必须满足一定条件。如图 5所示，透镜2与透镜3的安装基准距离L0，镜筒材料的线膨胀系数α，POM的线膨胀系数αpom，则Lpom应该满足公式：
$$ {\mathit{L}_{{\rm{pom}}}}({\mathit{\alpha }_{{\rm{pom}}}} - \mathit{\alpha }) + {\mathit{L}_0}\mathit{\alpha } = \Delta \mathit{L}/\Delta \mathit{T} $$ 为验证结构设计的合理性，通过有限元仿真分析不同环境温度下各透镜的间隔变化。对透镜与镜筒，透镜与隔圈等选择适合的约束，施加均匀温度场载荷，选取各透镜中心节点，获得不同温度下的位移量如表 3。与表 2相比误差≤0.02 mm，满足不同温度下间隔公差要求。
表 3 仿真分析不同温度下透镜3的位移Table 3. Shift of lens 3 under different temperature by simulationTemperature /℃ －40 20 60 Displacement /mm －0.053 0 0.032 4. 两种无热化方案对比
对比结构设计完成的两种无热化镜头，如表 4所示。可以发现混合被动无热化的成像质量、重量与光学被动无热化相当，但是体积和加工难度上明显优于光学被动无热化。从而证实，混合被动无热化技术可实现低成本、高性能的无热化效果。
表 4 两种无热化方案对比Table 4. Comparison of different athermalization methodsPassive optical athermalization Passive optical and mechanical athermalization Weight 356 g 354 g Volume φ75 mm×80 mm φ75 mm×75 mm MTF On axis≥0.42 On axis≥0.46 Out axis≥0.38 Out axis≥0.37 Distortion ≤0.7% ≤1.3% Complexity 3 aspheric surface
1 diffractive surface3 aspheric surface 5. 总结
针对某焦距75 mm，F/1长波非制冷无热化镜头的研制需求，分别利用光学被动无热化和混合被动无热化两种方式设计实现。对比两种镜头的体积、重量、加工难度、成像质量等，可以看出混合被动无热化可以有效降低被动无热化镜头的设计难度、加工成本和体积。从而证实，混合被动无热化技术适用于低成本、高质量的被动无热化镜头设计开发。
-
![]()
图 1 自抗扰控制系统的结构框图
Figure 1. Structural block diagram of active disturbance rejection control system
![]()
图 6 PFA控制算法50℃ Simulink仿真图
Figure 6. Simulation diagram of PFA control algorithm at 50℃ using Simulink
![]()
图 7 PFA控制算法—25℃ Simulink仿真图
Figure 7. PFA control algorithm -25℃ Simulink simulation diagram
![]()
图 12 2.4~4.5 μm谱段辐射定标示意图
Figure 12. Schematic diagram of radiation calibration in the 2.4-4.5 μm spectral range
表 1 PFA算法与传统算法的比较
Table 1 Comparison between PFA algorithm and traditional algorithm
Basic PID Fuzzy PID ADRC PFA Temp accuracy × √ × √ Faster response time √ √ × √ Faster stabilization time √ √ × √ Anti-interference ability × × √ √ Lower overshoot × × √ √ Application surface √ × × √ 
下载: 导出CSV
表 2 四种控制算法50℃下仿真效果比较
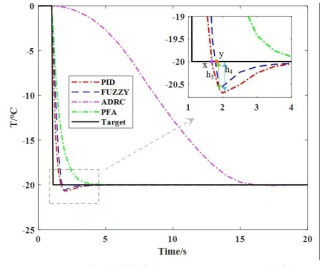
Table 2 Comparison of simulation effects of four control algorithms at 50℃
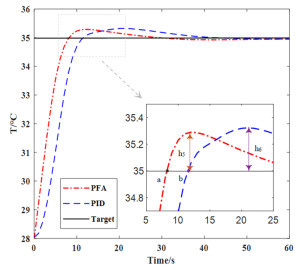
Algorithm Overshoot Response time/min Stable time/min Temperature control precision/mK Basic PID 3.606% 6.4 16 4 Fuzzy PID 3.036% 6.8 20 2 ADRC 0.205% 64 64 10 PFA 0.101% 14.4 16 1
下载: 导出CSV
表 3 35℃误差评估表
Table 3 35℃ error evaluation table
IAE assess ITAE assess PFA Algorithm 0.3902 3.2520 PID Algorithm 0.6067 4.8748
下载: 导出CSV
表 4 100℃误差评估表
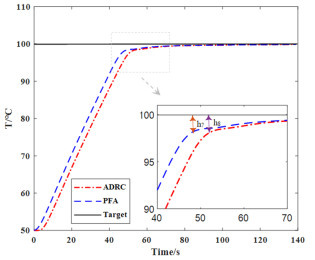
Table 4 100℃ error evaluation table
IAE assess ITAE assess PFA Algorithm 9.7455 193.2658 ADRC Algorithm 10.9575 230.7170
下载: 导出CSV
-
[1] 晋利兵, 李晓曼, 练敏隆, 等. 黑体与恒星相结合的短波红外遥感器在轨辐射定标简析[J]. 红外技术, 2023, 45(2): 123-128. http://hwjs.nvir.cn/cn/article/id/0fd611eb-5560-4d90-b2e5-4f60299ab871?viewType=HTML JIN Libing, LI Xiaoman, LIAN Minlong, et al. Analysis of in orbit radiation calibration of shortwave infrared remote sensors combining blackbody and stars[J]. Infrared Technology, 2023, 45(2): 123-128. http://hwjs.nvir.cn/cn/article/id/0fd611eb-5560-4d90-b2e5-4f60299ab871?viewType=HTML
[2] Morozova S P, Parfentiev N A, Lisiansky B E, et al. Vacuum variable-temperature blackbody VTBB100[J]. International Journal of Thermophysics, 2008, 29(1): 341-351. DOI: 10.1007/s10765-007-0355-z
[3] 杨词银, 曹立华. 大口径红外光电系统辐射定标及误差分析[J]. 红外与激光工程, 2011, 40(9): 1624-1628. https://www.cnki.com.cn/Article/CJFDTOTAL-HWYJ201109006.htm YANG Ciyin, CAO Lihua Radiation calibration and error analysis of large aperture infrared optoelectronic systems[J]. Infrared and Laser Engineering, 2011, 40(9): 1624-1628. https://www.cnki.com.cn/Article/CJFDTOTAL-HWYJ201109006.htm
[4] YANG D. Design of measurement and control system for a large blackbody radiation source [J]. Infrared, 2018, 8(8): 11-17.
[5] Sundayani, Dyan Franco Sinulingga, Fabiola Magdalena Prasetyawati, et al. PID temperature controlling of thermoelectric based cool box[C]//International Conference on Control, Electronics, Renewable Energy and Communications (ICCREC), 2017: 236-240.
[6] Guillermo Silva, Datta A, Bhattacharyya S P. New results on the Synthesis of PID Controllers[J]. IEEE Transactions on Automatic, 2002, 47(2): 241-252. DOI: 10.1109/9.983352
[7] Saad Kelam, Mohamed Chennafa, Mohammed Belkhiri. Nonlinear robust ADRC control of induction machine[J/OL]. Przeglad Elektrotechniczny, 2023: 209-215, http://www.pe.org.pl/articles/2023/3/37.pdf.
[8] Md Mizanur Rahman, Md Saiful Islam. Design of a fuzzy based pid algorithm for temperature control of an incubator[J]. Journal of Physics: Conference Series, 2021, 1969: 012055. DOI: 10.1088/1742-6596/1969/1/012055
[9] Zaiqi Y, Ning L, Kexin W, et al. Design of fuzzy PID Controller based on sparse fuzzy rule base for CNC machine tools[J]. Machines, 2023, 11(1): 81. DOI: 10.3390/machines11010081
[10] Jacek M, Kenton Graviss. A neural network controller for optimal temperature control of household refrigerators[J]. Intelligent Automation and Soft Computing, 1998, 4(4): 357-372. DOI: 10.1080/10798587.1998.10750743
[11] PAN H, XU Y. A new intelligent decoupling controller based on BP neural network PID with predictive compensation and the research on its application to an air-cushioned headbox[C]// 8th World Congress on Intelligent Control and Automation, 2010: 4731-4735.
[12] Thakor M D, Hadia S K, Kumar A. Precision temperature control through thermoelectric Cooler with PID controller[C]//International Conference on Communications and Signal Processing IEEE, 2015: 1118-1122.
[13] HUANG D X, WANG J H, WANG Z G. The temperature control of planar blackbody radiation source based on nonlinear PID[C]//Advances in Energy, Environment and Materials Science, 2016: 139-144.
[14] 韩京清. 从PID技术到"自抗扰控制"技术[J]. 控制工程, 2002, 9(3): 13-18. https://www.cnki.com.cn/Article/CJFDTOTAL-JZDF200203004.htm HAN Jingqing. From PID technology to self disturbance rejection control technology[J]. Control Engineering, 2002, 9(3): 13-18. https://www.cnki.com.cn/Article/CJFDTOTAL-JZDF200203004.htm
[15] ZHOU Keliang, YU Hongyan. Application of fuzzy predictive-PID control in temperature control system of Freeze-dryer for medicine material[C]//Second International Conference on Mechanic Automation and Control Engineering, 2011: 7200-7203.
[16] Cetin S, Akkaya A V. Simulation and hybrid fuzzy-PID contorl for positioning of a hydraulic system[J]. Nonlinear Dynamics, 2015, 61(3): 465-470.
[17] ZHU Z H, SUN H Y. Application of PID controller based on BP neural network in export steam's temperature control system[J]. Journal of Measurement Science & Instrumentation, 2011, 2(1): 84-87.
[18] WANG Z, LI X, LU X. Temperature control based on a single neuron PID algorithm for a blackbody radiation source[C]//IEEE International Conference on Mechatronics and Automation(ICMA), 2017: 220-225.
[19] WU Q, LI X. PID controller parameter setting based on MATLAB/Simulink[J]. Electronic World, 2018, 544(10): 70-71.
[20] Arrieta O, Visioli A, Vilanova R. PID auto-tuning for weighted servo/regulation control operation[J]. Journal of Process Control, 2010, 4(20): 472-480.
[21] 姚立平, 刘伟章, 吴文明, 等. 一种引入滤波的PID控制算法在温控系统的应用[J]. 电子技术应用, 2022, 48(6): 79-83. https://www.cnki.com.cn/Article/CJFDTOTAL-DZJY202206018.htm YAO Liping, LIU Weizhang, WU Wenming, et al. Application of a PID control algorithm with filtering in temperature control systems[J]. Electronic Technology Applications, 2022, 48(6): 79-83. https://www.cnki.com.cn/Article/CJFDTOTAL-DZJY202206018.htm
[22] Aftab M S, Shafiq M. Adaptive PID controller based on Lyapunov function neural network for time delay temperature control[C]//GCC Conference and Exhibition, IEEE, 2015: 1-6.
-
期刊类型引用(5)
1. 刘鑫，王晶锦，刘庆梅，姜子康，徐兆鹏，李晓英. 大视场长波红外光学系统混合无热化设计. 红外与激光工程. 2025(02): 120-128 . 
百度学术
2. 吕阳，辛宏伟，康玉思，贺玉坤，陈长征. 红外与可见光双模导引头光学系统设计. 红外技术. 2024(01): 27-30 . 本站查看
3. 张丽芝，陆秋萍，段帆琳，戴幸，乔大勇. 长焦镜头光学系统设计及无热化研究. 光学学报. 2024(08): 227-236 . 百度学术
4. 刘朋朋，靳利锋，赵慧，李妥妥. 低轨道遥感相机光机热一体化分析及优化设计. 红外技术. 2022(06): 614-621 . 本站查看
5. 冯丽军，李训牛，陈洁，周玲玲，董江涛，孙爱平，鲍佳男. 大相对孔径大面阵长波红外光学无热化镜头的设计. 红外技术. 2022(10): 1066-1072 . 本站查看
其他类型引用(2)
计量
- 文章访问数: 78
- HTML全文浏览量: 19
- PDF下载量: 26
- 被引次数: 7
