Fast Finger Vein Recognition Based on a Dual Dimension Reduction Histogram of Oriented Gradient and Support Vector Machine
-
摘要: 为减少手指静脉识别时间，提出一种双重降维方向梯度直方图特征（Histogram of Oriented Gradient，HOG）结合支持向量机（Support Vector Machine，SVM）分类的手指静脉识别方法。针对传统HOG算法特征维数高的问题，首先通过Fisher准则衡量梯度方向区间HOG特征的分类能力，然后使用序列前向选择法挑选出分类能力较优异的梯度方向区间构建部分方向区间HOG特征，最后使用主成分分析（Principal Component Analysis，PCA）降维。在公开的手指静脉数据库FV-USM和THU-FV上使用SVM多分类器进行分类识别，实验结果表明：双重降维HOG方法相较于HOG+PCA方法提取的特征维数降低了40%，识别时间减少了29.85%，识别准确率分别为99.17%和100%，等误率分别为1.07%和0.01%。Abstract: An identification model using a dual-dimension reduction histogram of oriented gradients (HOG) combined with a support vector machine (SVM) is proposed to reduce the time required for finger vein recognition. To solve the problem of high feature dimensionality in the traditional HOG algorithm, the classification ability of the gradient direction interval is first measured using the Fisher criterion. Next, the sequence forward selection method is used to select the gradient direction interval with optimal classification ability to construct a partial direction interval HOG feature. Finally, principal component analysis (PCA) is used to reduce the number of dimensions. An SVM multi-classifier was used for the classification of the FV-USM and THU-FV datasets. The experimental results demonstrate that compared to the HOG+PCA method, the feature dimensions extracted by the dual-dimensional reduction HOG method are reduced by 40%, the recognition time is reduced by 29.85%, the recognition accuracy is 99.17% and 100%, respectively, and the equal error rate is 1.07% and 0.01%, respectively.
-
Keywords:
- finger vein recognition /
- HOG /
- feature selection /
- PCA /
- SVM
-
0. 引言
手指静脉识别技术使用手指内部的静脉作为特征信息，使用近红外光作为光源进行图像采集，相比于传统的人脸识别和指纹识别方式，具有活体性、高稳定性和高安全性，在银行、监狱以及老年医疗等场合有着极大的优势。近年来手指静脉识别技术成为生物特征识别领域的研究热点。
现有对手指静脉识别的研究方法中，常采用基于纹路拓扑结构的模板匹配方法[1-2]，首先从手指静脉图像中分割出静脉拓扑结构作为特征信息，然后计算模板间的Hausdorff距离进行匹配识别。但是此方法鲁棒性较差，识别准确率容易受光照和图像背景噪声等因素的影响。除了基于纹路拓扑结构的模板匹配方法外，还有神经网络方法[3-4]和局部特征描述方法[5-6]。基于神经网络的方法，无需对手指静脉进行特征提取[7]，可以根据已有的数据集学习到有价值的信息特征，然后对待识别手指静脉图像进行识别。但是神经网络方法对数据集的数据量要求比较高，当训练数据集的数据量较少时，所训练的网络识别效果欠佳。局部特征描述方法主要包括局部二值模式[8]（Local Binary Pattern，LBP）和方向梯度直方图[9]（histogram of oriented gradient，HOG），此类方法使用局部特征描述算子对手指静脉特征进行编码获得图像特征，然后使用支持向量机[10]（support vector machines，SVM）、线性判别分析[11]（linear discriminant analysis，LDA）、adaboost[12]等方法进行分类识别。文献[8]使用改进LBP描述符提取手指静脉特征，时间远高于HOG方法。虽然HOG特征提取时间开销少，但是采用部分区域重叠的方法逐区域进行特征提取[13]使得特征的维度非常高，导致后续特征识别过程的计算复杂度高，增加了识别过程的时间开销。文献[14]引入Harr积分图简化HOG计算过程，减少了特征提取时间，但没有解决HOG特征维数高的问题。文献[9]使用主成分分析（Principal Component Analysis，PCA）算法对手指静脉HOG特征降维后进行分类，特征识别时间有明显改善。但是PCA针对全局HOG特征进行降维，降维准则是保留对方差贡献度大的特征，未考虑局部的HOG特性，存在降维不充分的问题。
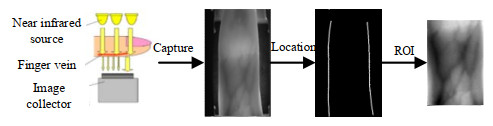
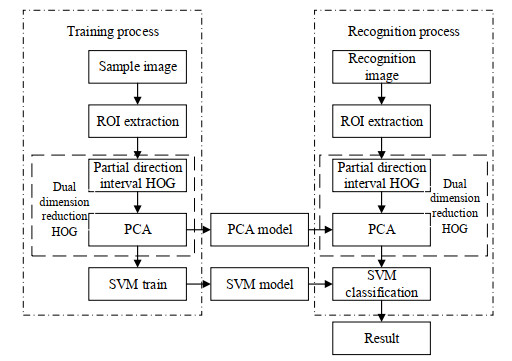
鉴于上述分析，本文提出一种双重降维HOG特征结合SVM分类的手指静脉识别模型，模型的总体结构如图 1所示。首先，使用Sobel边缘检测算法提取手指静脉图像的感兴趣区（region of interest，ROI）。其次，使用序列前向选择法挑选出识别能力较优异的梯度方向区间构建部分方向区间HOG特征，并使用PCA降维输出PCA子空间模型。然后，使用SVM对降维后的特征训练输出SVM分类模型。最后，使用训练过程输出的PCA子空间模型和SVM分类模型识别待识别图像。
1. 双重降维HOG手指静脉特征提取
1.1 ROI提取
静脉中的血红蛋白对近红外光的吸收能力较强，通常使用近红外光作为光源来采集手指静脉图像。采集到的手指静脉图像进行预处理，定位手指静脉图像感兴趣区，去除背景区域，有利于后续进行特征提取。本文使用Sobel边缘检测算法定位手指边缘，利用手指边缘信息和手指指节信息提取感兴趣区域，最后将感兴趣区尺寸标准化，过程如图 2所示。
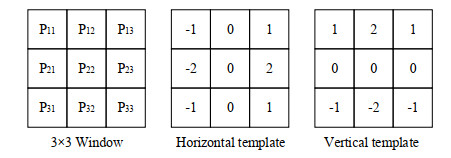
Sobel边缘检测算法使用区域模板与图像进行卷积得到图像在两个方向上的梯度Gx、Gy，然后对两个方向上的梯度求模得到梯度幅值G，通过梯度幅值与预设的阈值进行比较来确定图像的边缘。使用图 3中模板计算的过程如式(1)、(2)、(3)。
$$ G_{x}=(P_{13}+2P_{23}+P_{33})-(P_{11}+2P_{21}+P_{31})$$ (1) $$ G_{y}=(P_{11}+2P_{12}+P_{13})-(P_{31}+2P_{32}+P_{33}) $$ (2) $$ G = \sqrt {G_x^2 + G_y^2} $$ (3) 1.2 部分方向区间HOG特征
HOG特征是一种基于图像局部梯度信息统计的特征描述符，其理论依据是一幅图像中的局部形状和边缘特征能够被梯度方向和梯度幅值所描述。
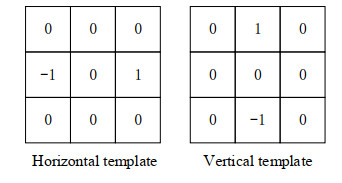
使用图 4所示Sobel模板对图像做卷积运算，计算像素点水平方向和垂直方向的梯度幅值Gx、Gy，根据两个方向上的梯度计算像素点的梯度幅值G和梯度方向θ：
$$ \theta = \arctan \left( {\frac{{{G_y}}}{{{G_x}}}} \right) $$ (4) 将梯度方向范围均匀分成9个方向区间，每个方向区间对应cell直方图的一个特征维度，根据像素点的梯度信息将其投影至直方图的对应特征维度中，投影权重为像素点的梯度幅值。按照cell、block和图像三者间的构成关系，分别将所有cell中相同的方向区间特征进行串联，得到9个单方向区间HOG特征向量。
以Fisher准则作为衡量标准，将9个单方向区间HOG特征向量按照Fisher值从大到小排列。Fisher准则寻求一个最优子空间使样本类间散度尽量大，类内散度尽量小，二者比值越大说明分类能力越强。Fisher计算公式如式(5)所示：
$$ F = \max \frac{{{\text{tr}}({\boldsymbol{W}^{\text{T}}}{\boldsymbol{S}_{\text{b}}}\boldsymbol{W})}}{{{\text{tr}}({\boldsymbol{W}^{\text{T}}}{S_{\text{w}}}\boldsymbol{W})}} $$ (5) 式中：tr(·)是矩阵迹运算；W是样本进行线性变换的子空间；Sb是样本的总类间散度；Sw是样本的总类内散度。总类间散度和总类内散度的计算方法如式(6)和式(7)所示：
$$ {\boldsymbol{S}_{\text{b}}} = \sum\limits_{i = 1}^n {{n_i}{{({{\bar x}_i} - \bar x)}^{\text{T}}}} ({\bar x_i} - \bar x) $$ (6) $$ {\boldsymbol{S}_{\text{w}}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^{{n_i}} {{{({x_{i,j}} - {{\bar x}_i})}^{\text{T}}}} } ({x_{i,j}} - {\bar x_i}) $$ (7) 式中：n为手指静脉样本的类别数；ni为第i类的样本数目；${\bar x_i}$为第i类的样本均值；$\bar x$为全部样本的样本均值；xi, j为第i类中的第j个样本。
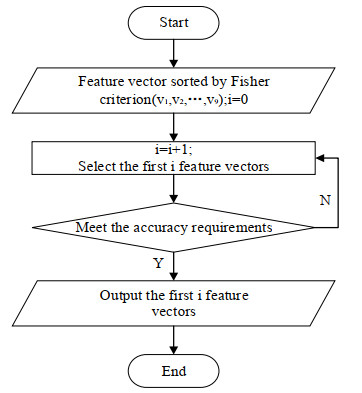
使用序列前向选择法选择单方向区间HOG特征向量中的i个构建部分方向区间HOG特征向量。序列前向选择法流程如图 5所示，依次增加排序后的单方向区间HOG特征的数目，直到分类准确率满足要求。
1.3 PCA降维
PCA把原始的n维特征映射到k维空间上，映射后的k维是在原有n维特征的基础上构建出的全新的正交特征，在降低数据集维数的同时保留了对数据集的方差贡献度最大的特征。
根据公式(8)计算手指静脉样本库的部分方向HOG特征向量的协方差矩阵。求取协方差矩阵的特征值λ=(λ1, λ2, …, λn)及其对应的特征向量V=(v1, v2, …, vn)，并根据特征值降序排列特征向量。
$$ {S_{\text{t}}} = \frac{1}{m}(\boldsymbol{X} - \boldsymbol{\bar X}){(\boldsymbol{X} - \boldsymbol{\bar X})^{\text{T}}} $$ (8) 式中：m为样本数量；X为样本特征向量；$\boldsymbol{\bar X}$为样本均值。
根据公式(9)计算协方差矩阵特征值的累计贡献率，贡献率取值通常取85%~99%之间，根据贡献率取值要求选择前k个较大的特征值所对应的特征向量Vk=(v1, v2, …, vk)作为主成分分析的特征子空间的投影矩阵Wpca=(v1, v2, …, vk)。最后将输入数据投影至子空间。
$$ R = {{\sum\limits_{i = 1}^k {{\lambda _i}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^k {{\lambda _i}} } {\sum\limits_{j = 1}^n {{\lambda _j}} }}} \right. } {\sum\limits_{j = 1}^n {{\lambda _j}} }} $$ (9) 2. 基于SVM的手指静脉识别
支持向量机通过寻找一个超平面把两类样本完全分开并且两类间的几何间隔最大。设超平面的方程式为：w·x+b=0，则可以把w·x+b＞0的数据归为1类，把w·x+b＜0的数据归为-1类。支持向量机求解超平面问题可以表示为式(10)所示的约束最优化问题：
$$ \begin{gathered} J(w,b,\varepsilon ) = \mathop {\min }\limits_{w,b} \frac{1}{2}||w|{|^2} + C\sum\limits_{i = 1}^n {{\varepsilon _i}} \hfill \\ {\text{s}}{\text{.}}{\kern 1pt} {\kern 1pt} {\text{t}}{\text{.}}{\kern 1pt} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_i}(w \cdot x + b) \geqslant 1 - {\varepsilon _i},{\varepsilon _i} \gt 0,i = 1,2, \cdots ,n \hfill \\ \end{gathered} $$ (10) 式中：惩罚因子C和松弛变量ε用于对目标函数和约束条件进行修正。引入拉格朗日乘子α，超平面参数w和b可以使用对偶问题的解α来确定，由此可以得到支持向量机的最优分类函数：
$$ f(x) = \text{sgn} (\sum\limits_{i = 1}^n {{a_i}{y_i}K({x_i} \cdot x) + b} ) $$ (11) 式中：K为核函数，用于解决非线性分类问题，常用的核函数有线性核函数（Linear Kernel）、多项式核函数（polynomial kernel）、径向基核函数（RBF kernel）和sigmoid核函数（sigmoid kernel）。在训练集对4种核函数进行测试，相关指标如表 1所示，线性核函数训练的支持向量数量少于其他3种，识别准确率最高。此外线性核函数复杂度较低，故本文设计分类器使用线性核函数。
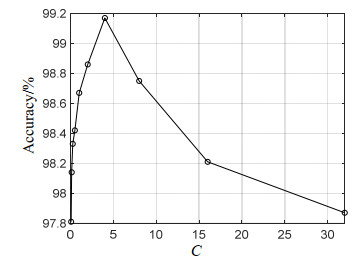
表 1 核函数分类训练数据Table 1. Training data of kernel functionKernel Number of support vectors Accuracy MIN MAX Linear 5 8 98.67% Polynomial 8 8 75.17% RBF 8 8 97.83% Sigmoid 8 8 97.83% 基于线性核函数的支持向量机还需要确定惩罚因子C来获取更好的识别性能。使用倍增的惩罚因子2-4, 2-3, 2-2, 2-1, 20, 21, 22, 23, 24进行测试，分类器识别准确率如图 6所示，在惩罚因子为4时识别准确率达到最高，因此选用C=4作为支持向量机的惩罚因子。
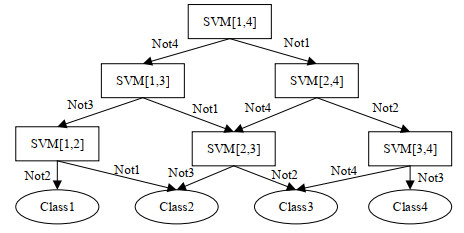
实际应用中，手指静脉识别过程为多分类问题，基本的二分类SVM模型无法满足实际需求。本文对任意两类手指静脉都训练一个二分类SVM模型，并根据决策函数确定二分类SVM的分类结果。最后，对所有的二分类SVM模型的分类结果进行投票表决，得票数最多的分类结果即为多分类SVM的分类结果。图 7所示为基于二分类SVM的四分类器，其中SVM[i, j]为使用第i类和第j类样本训练的二分类器。
3. 实验与分析
本文使用的计算机配置为8.0 G内存和1.6 GHz主频CPU，实验平台为Matlab2018a，使用的数据集为马来西亚理工大学的FV-USM手指静脉数据库和清华大学的THU-FV手指静脉数据库。FV-USM数据库中共有492个分类，每个分类在两个阶段共采集12张图像。THU-FV数据库中共有610个分类，每个分类采集8张图像。本文实验将每个分类中的前4张图像作为训练样本，其余作为测试样本，所有图像尺寸标准化为128×64像素。
3.1 方向区间数目的确定
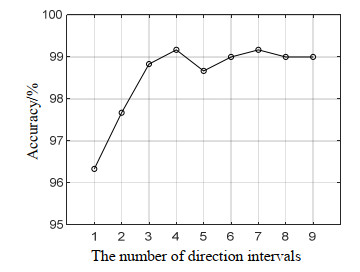
为确定部分方向区间HOG特征中包含的方向区间数目，本文使用FV-USM数据集中的手指静脉图像进行实验，得到方向区间数目与手指静脉识别准确率的关系如图 8所示。从图中可知，选择前3个方向区间时的识别准确率为98.83%，十分接近包含9个方向区间的传统HOG的识别准确率99.02%，选择前4个方向区间的识别准确率首次取得最大值99.17%。继续增加方向区间数目，识别准确率非但没有增加，反而在某些组合情况下出现轻微下降。原因在于不同的方向区间HOG特征向量之间存在相关性，后续增加的特征没有提供新的更具区分能力的信息，反而可能引入噪声信息，导致识别准确率降低。综上所述，后续实验中部分方向区间HOG特征包含的方向区间数目确定为4。
![]()
图 8 方向区间数目与识别准确率关系图Figure 8. Relationship between the number of direction intervals and the recognition accuracy3.2 时间开销分析
为评估本文提出的双重降维HOG特征提取方法，将其与经典的局部特征算法LBP和HOG以及HOG+PCA方法在FV-USM数据库上进行实验，结果如表 2所示。LBP算法的特征提取时间远高于HOG算法的提取时间，原因在于LBP算法对于每个像素点要与周围的8个像素点进行比较后进行编码和直方图统计，计算量大。本文提出的双重降维HOG方法的特征提取时间开销略高于传统HOG算法，与HOG+PCA方法基本持平，原因在于本文提出的双重降维HOG特征没有改变HOG算法的编码原理，增加的仅是特征降维的过程。在识别时间方面，可以发现支持向量机识别时间与特征维数呈正相关关系，本文提出的双重降维HOG方法提取的特征维数最少，相比于传统HOG+PCA算法特征维数降低了40%，特征识别时间减少了29.85%。
表 2 时间开销比较Table 2. Comparison of time costMethods Dimension of feature Extraction time/ms Recognition time/ms LBP+SVM 1152 798.64 98.32 HOG+SVM 672 25.73 35.73 HOG+PCA+SVM 145 26.76 19.10 Proposed method 87 26.97 13.59 3.3 识别性能分析
准确率（Accuracy）和等误率（equal error rate，EER）是手指静脉识别研究中常用的性能指标。准确率是测试时正确识别次数所占的比率，表示模型对当前数据集的适用程度。等误率是拒识率（false rejection rate，FRR）和误识率（false accept rate，FAR）近似相等时的拒识率或误识率，等误率的数值越小，说明识别效果越好。
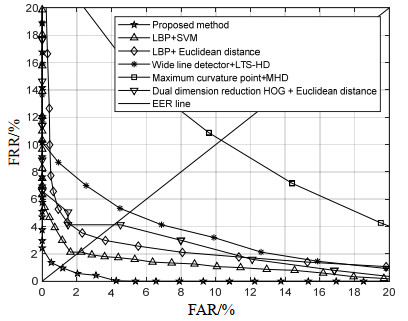
为评估本文提出的手指静脉识别模型，将提出的算法模型与其他方法在FV-USM和THU-FV数据库上进行测试，数据如表 3所示，图 9为根据FV-USM数据库的测试结果绘制的使用接受者操作特性（receive operating characteristic，ROC）曲线图。从实验数据中可以看出，本文提出的方法在两个数据库上都取得了最优的准确率和等误率，原因在于：在特征构建过程中，依据Fisher准则选择特征，使样本类内散度尽量小，类间散度尽量大；使用PCA保留对样本方差贡献度大的特征。表 3中最后4组数据将欧式距离计算相似度的识别方法和SVM分类的识别方法进行对比，结果显示使用SVM分类可以获取更好的识别性能，原因在于SVM通过核函数将线性不可分的数据映射到高维空间进行求解，并通过改变惩罚因子的值来寻求更优的分类能力。
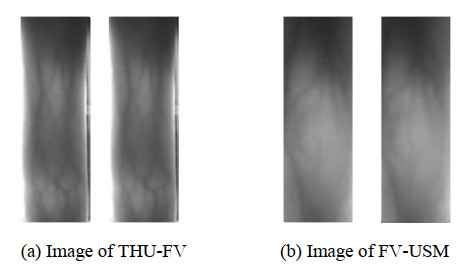
表 3 不同方法实验数据比较Table 3. Comparison of experimental data of different methodsMethods FV-USM THU-FV Accuracy/% EER/% Accuracy/% EER/% Maximum curvature point+MHD 87.64 10.46 98.38 2.12 Wide line detector+LTS-HD 92.38 5.35 99.26 0.34 LBP+ Euclidean distance 96.13 3.66 100 0.32 Dual dimension reduction HOG+ Euclidean distance 97.26 4.12 100 0.28 LBP+SVM 97.86 2.16 100 0.04 Proposed method 99.17 1.07 100 0.01 实验中各种方法在THU-FV数据库的实验数据优于FV-USM数据库的数据，是因为THU-FV数据库中的手指静脉图像质量高并且来自同一手指的不同图像间的差异极小，而FV-USM数据库的图像较为模糊，静脉纹路不明显，具体图像如图 10所示。此外最大曲率+MHD方法和宽线检测+LTS-HD方法都是基于静脉纹路分割的手指静脉识别方法，由于FV-USM数据库中静脉纹路比较模糊不易分割出完整的静脉纹路拓扑，导致算法的识别准确率和等误率数据较差。
4. 结语
本文提出一种双重降维HOG特征结合SVM分类的手指静脉识别模型。依据Fisher准则衡量各梯度方向区间的分类能力，并使用序列前向选择法挑选出分类能力强的梯度方向区间的组合构建部分方向区间HOG特征，实现HOG特征的第一次降维。对部分方向HOG特征使用PCA降维，实现HOG特征的第二次降维。基于二分类SVM构建多分类器用于所提取特征的分类识别。在公开的手指静脉数据库FV-USM和THU-FV上进行实验的结果表明：本文提出的双重降维HOG特征方法能够有效降低特征维数，使用SVM分类识别的时间有明显改善，并且获得了较高的识别准确率和较低的等误率，能够实现手指静脉的精准识别。
-
![]()
图 8 方向区间数目与识别准确率关系图
Figure 8. Relationship between the number of direction intervals and the recognition accuracy
表 1 核函数分类训练数据
Table 1 Training data of kernel function
Kernel Number of support vectors Accuracy MIN MAX Linear 5 8 98.67% Polynomial 8 8 75.17% RBF 8 8 97.83% Sigmoid 8 8 97.83% 
下载: 导出CSV
表 2 时间开销比较
Table 2 Comparison of time cost
Methods Dimension of feature Extraction time/ms Recognition time/ms LBP+SVM 1152 798.64 98.32 HOG+SVM 672 25.73 35.73 HOG+PCA+SVM 145 26.76 19.10 Proposed method 87 26.97 13.59
下载: 导出CSV
表 3 不同方法实验数据比较
Table 3 Comparison of experimental data of different methods
Methods FV-USM THU-FV Accuracy/% EER/% Accuracy/% EER/% Maximum curvature point+MHD 87.64 10.46 98.38 2.12 Wide line detector+LTS-HD 92.38 5.35 99.26 0.34 LBP+ Euclidean distance 96.13 3.66 100 0.32 Dual dimension reduction HOG+ Euclidean distance 97.26 4.12 100 0.28 LBP+SVM 97.86 2.16 100 0.04 Proposed method 99.17 1.07 100 0.01
下载: 导出CSV
-
[1] YANG L, YANG G P, YIN Y L, et al. Finger vein recognition with anatomy structure analysis[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2018, 28(8): 1892-1905. https://ieeexplore.ieee.org/document/7882665
[2] CHEN G H, DAI QH, TANG X, et al. An improved least trimmed square hausdorff distance finger vein recognition[C]//International Conference on Systems and Informatics (ICSAI), 2018: 939-943.
[3] LI S Y, ZHANG H G, YANG JF. Finger vein recognition based on local graph structural coding and CNN[C]//Proc of SPIE, 2019, 11069: 110693I-110693I-8.
[4] ZHANG Y K, LI W J, ZHANG L P, et al. Adaptive Gabor convolutional neural networks for finger-vein recognition[C]//International Conference on High Performance Big Data and Intelligent Systems (Hpbd & Is), 2019: 219-222.
[5] LIU H Y, YANG L, YANG G P, et al. Discriminative binary descriptor for finger vein recognition[J]. IEEE Access, 2018, 6: 5795-5804. DOI: 10.1109/ACCESS.2017.2787543
[6] WANG X, WANG H B, HE Y, et al. Novel Algorithm for finger vein recognition based on inception-Resnet module[J]. Proc of SPIE, 2019, 11179: 111791D-111791D-9.
[7] 陶志勇, 胡亚磊, 林森. 基于改进AlexNet的手指静脉识别[J]. 激光与光电子学进展, 2020, 57(8): 58-66. https://www.cnki.com.cn/Article/CJFDTOTAL-JGDJ202008007.htm TAO Zhiyong, HU Yalei, LIN Sen. Finger vein recognition based on improved AlexNet[J]. Laser & Optoelectronics Progress, 2020, 57(8): 58-66. https://www.cnki.com.cn/Article/CJFDTOTAL-JGDJ202008007.htm
[8] 刘超, 王容川, 许晓伟, 等. 基于改进LBP的手指静脉识别算法[J]. 计算机仿真, 2019, 36(1): 381-386. DOI: 10.3969/j.issn.1006-9348.2019.01.079 LIU Chao, WANG Rongchuan, XU Xiaowei, et al. Finger vein recognition algorithm based on improved LBP[J]. Computer Simulation, 2019, 36(1): 381-386. DOI: 10.3969/j.issn.1006-9348.2019.01.079
[9] 李菲, 李小霞, 周颖玥. 基于改进HOG特征和稀疏表示的手指静脉识别[J]. 传感器与微系统, 2018, 37(11): 38-41. https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ201811011.htm LI Fei, LI Xiaoxia, ZHOU Yingyue. Finger vein recognition based on improved HOG features and sparse representation[J]. Transducer and Microsystem Technologies, 2018, 37(11): 38-41, 44. https://www.cnki.com.cn/Article/CJFDTOTAL-CGQJ201811011.htm
[10] Veluchamy S, Karlmarx L R. System for multimodal biometric recognition based on finger knuckle and finger vein using feature-level fusion and k-support vector machine classifier[J]. IET Biometrics, 2017, 6(3): 232-242. DOI: 10.1049/iet-bmt.2016.0112
[11] 徐子豪, 陈光化, 傅志威. 改进型LDA结合LBP的手指静脉识别[J]. 现代电子技术, 2020, 43(12): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-XDDJ202012002.htm XU Zihao, CHEN Guanghua, FU Zhiwei. Finger vein recognition of improved LDA combined with LBP[J]. Modern Electronics Technique, 2020, 43(12): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-XDDJ202012002.htm
[12] 徐铸业, 赵小强. 基于Agast-Adaboost的图像匹配算法[J]. 兰州理工大学学报, 2020, 46(4): 110-115. DOI: 10.3969/j.issn.1673-5196.2020.06.001 XU Zhuye, ZHAO Xiaoqiang. Image matching algorithm based on Agast-Adaboost[J]. Journal of Lanzhou University of Technology, 2020, 46(6): 1-4. DOI: 10.3969/j.issn.1673-5196.2020.06.001
[13] 贾楚. 基于改进HOG特征的行人检测算法研究[D]. 秦皇岛: 燕山大学, 2016. JIA Chu. Research of Pedestrian Detection Based on Improved HOG Features[D]. Qinhuangdao: Yanshan University, 2016.
[14] 蒋政, 程春玲. 基于Haar特性的改进HOG的人脸特征提取算法[J]. 计算机科学, 2017, 44(1): 303-307. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201701057.htm JIANG Zheng, CHENG Chunling. Improved HOG face feature extraction algorithm based on Haar characteristics[J]. Computer Science, 2017, 44(1): 303-307. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201701057.htm
-
期刊类型引用(3)
1. 傅莉，吉宏轩，张宇峰，任艳. 基于感知哈希算法的特征融合玻璃瓶缺陷检测. 无线电工程. 2024(01): 55-62 . 
百度学术
2. 马莉，刘子良，谭振林，黄蔼权，杨文茵. 一种轻量级掌静脉识别算法NEPVR. 计算机技术与发展. 2024(12): 213-220 . 百度学术
3. 李杰，瞿中. 深度学习在手指静脉识别中的应用研究综述. 计算机科学与探索. 2023(11): 2557-2579 . 百度学术
其他类型引用(8)
计量
- 文章访问数: 135
- HTML全文浏览量: 38
- PDF下载量: 22
- 被引次数: 11
