Infrared Spectral Noise Reduction Algorithm Based on Wavelet Transform Optimized EEMD Combined with SG
-
摘要:
红外光谱气体分析技术由于具有检测参数多、检测效率高、分析准确等优势,已经逐渐成为气测录井的主要分析手段。但是由于地层流体中的烃类气体种类多、浓度范围跨度大等因素,致使测量的光谱数据复杂,所以光谱数据的预处理尤为重要,这直接关系到测量结果的准确性,而噪声是一个极为重要的干扰因素,如何对得到的烃类光谱数据进行去噪处理是一个至关重要的问题。基于此,本文提出了小波变换优化集合经验模态分解(EEMD)结合Savitzky-Golay滤波(S-G)的红外光谱降噪算法,该算法首先利用EEMD对信号进行分解得到多个IMF分量,再利用小波变换对各IMF分量进行小波阈值去噪,最后对去噪后的各IMF分量进行重构并进行S-G滤波。实验结果表明,本文提出的算法能够同时有效的去除吸收光谱数据中高斯白噪声和脉冲噪声,还提高了吸收光谱的平滑度指标,提升了录井气体检测的准确性。
-
关键词:
- 气测录井 /
- 去噪 /
- 小波变换 /
- EEMD /
- Savitzky-Golay滤波
Abstract:Infrared spectral gas analysis technology has gradually become the main analytical method for gas logging owing to its advantages of non-pollution, high detection efficiency, and accurate analysis. However, because of factors, such as numerous types of hydrocarbon gases in the formation fluid and a large concentration range span, the measured spectral data are complicated. Therefore, the pre-processing of the spectral data is crucial as it directly impacts the accuracy of the measurement results. Noise is a significant interference factor, and improving the noise reduction process for the spectral data is crucial. To solve this problem, this study proposes a wavelet transform optimized ensemble empirical mode decomposition (EEMD) combined with Savitzky-Golay filtering (S-G) for the infrared spectral noise reduction algorithm. This algorithm first uses EEMD to decompose the signal to obtain a set of IMF components. It then uses wavelet transform for wavelet threshold denoising on the IMF components. Finally, the denoised IMF components are reconstructed, followed by S-G. The experimental results show that the algorithm can not only remove the Gaussian white noise and impulse noise in the absorption spectrum but also improve the smoothness index of the absorption spectrum and enhance the accuracy of logging gas detection.
-
Keywords:
- gas logging /
- denoising /
- wavelet transform /
- EEMD /
- avitzky-Golay filtering
-
0. 引言
红外吸收光谱,其检测原理基于朗伯比尔定律分析出射光线被待测物质吸收的情况,通过解析红外吸收光谱图中吸收峰特征来定量分析待测物质的组分信息。与传统的气相色谱检测技术相比,基于光谱的录井检测技术有诸多突出的优势,如能够实现快速检测、稳定性好、检测成本低等,更重要的是光谱录井技术在检测时可以对混合组分气体检测,不需要对气体提前进行分离[1]。
由于地层流体中的烃类气体种类多、浓度范围跨度大,环境干扰等因素,致使测量的光谱数据复杂,通常包含大量的噪声信息,这些噪声导致吸收光谱数据失真,尤其是当烃类气体含量较低时,甚至会淹没有用信号,极大地影响烃类组分的定量结果[2-4]。因此,为去除噪声的影响,得到准确度较高的光谱数据,必须对测量得到的吸收光谱数据进行去噪处理。
近年来,很多学者在红外光谱去噪领域有着广泛深入的研究。1998年,Huang提出了经验模态分解方法(empirical mode decomposition, EMD),该方法依托信号本身进行分解,对于处理庞大数据量的非线性信号,可以极大地保证信号的完整性同时将信号分解成多个时频段。但是处理频率变化较快的间歇信号存在模态混叠现象[5]。为解决EMD存在的缺陷,2009年,WU等人提出了集合经验模态分解方法(ensemble empirical mode decomposition, EEMD),但是该方法在处理某些信号时又存在精确度不稳定的缺陷[6]。2015年,刘铭华分别将EMD、EEMD及小波3种方法应用于甲烷的红外光谱中,从去噪后的数据可以看出,EEMD的去噪效果最佳,但EEMD在使用中需要依靠经验来选取有效的IMF(intrinsic mode function)分量[7];2019年,王书涛等人提出了使用小波变换优化EEMD的去噪算法,该算法克服了EEMD中IMF分量依靠经验来选取的缺点,最大地保留了高频信号中的有用信号,但未考虑脉冲噪声的影响[8]。
针对现有算法中存在的问题,包括模态混叠、IMF分量依靠经验选取、未考虑脉冲噪声等问题。本文提出了小波变换优化集合经验模态分解(EEMD)结合Savitzky-Golay(SG)滤波的红外光谱降噪算法,该算法首先利用EEMD对信号进行分解得到多个IMF分量,再利用小波变换对各IMF分量进行小波阈值去噪,最后对去噪后的各IMF分量进行重构并进行Savitzky-Golay滤波。
1. 相关工作
1.1 小波变换去噪
小波分析是在傅里叶变换的基础上发展而来的,在分析信号方面具有其他方法所不具备的优势,属于时频分析方法,是光谱去噪分析的常用方法,广泛用于与信号分析和图像处理领域[9]。小波分析去噪的基本原理是通过将原始信号分解成不同频率和方向的分量,再根据阈值对有效信息进行提取[10-11]。
小波去噪一般分为3个步骤:
① 信号分解,选择一种小波函数并对信号进行N层分解;②选择合理阈值对分解得到各层的系数进行阈值量化处理去噪;③信号重构,得到去噪后的信号。
1.2 EEMD
EEMD方法是一种通过叠加高斯白噪声的经验模式分解,其利用了高斯白噪声具有频率正态分布的统计特性,通过每次加入同幅值、频率不同的白噪声来改变信号的极值点特性,之后对多次EMD得到的相应IMF分量进行总体平均来抵消加入的白噪声,从而对模态混叠的产生进行抑制[12-15]。其具体分解实现步骤如下:
① 随机产生幅值相同,频率不同的高斯白噪声φi(t)并加入到原始信号x(t)中以产生一个新的信号:
$$ x_{i}(t)=x(t)+y(t) $$ (1) ② 将得到的含高斯白噪声的信号xi(t)分别利用EMD方法逐一分解,得到多个不同的IMF分量,记为IMFni,i=1, 2, 3…, M,n=1, 2, 3…, N,其中n为分解尺度。
③ 将步骤②得到的多个IMF分量进行总体平均运算,即可得到EEMD分解的最后结果,即:
$$ \mathrm{IMF}_{n} = \frac{1}{M}\sum\limits_{i = 1}^M {\mathrm{IMF}_n^i} $$ (2) 1.3 Savitzky-Golay滤波去噪
Savitzky-Golay算法是由Savitzky A.和Golay M.提出的一种数字滤波器,在光谱数据平滑去噪上有着较好的效果。它是通过移动窗口利用线性最小二乘法进行拟合的滤波算法。S-G算法是使用最小二乘法和移动窗口的方式得到多项式系数,然后求解多项式数值来得到处理结果。此外,该方法可由卷积系数表确定多项式系数,从而达到根据多项式函数来获得去除噪声的目的[16-18]。
假设有一组数据x(i),窗口宽度为2n+1个连续的整值i,即,i=-n, …, 0, …, n。再构造一个m阶多项式(m≤2n+1)对该组数据进行拟合,公式如下:
$$ {f_i} = \sum\limits_{k = 0}^m {{a_{mk}}} {i^k} = {a_{m0}}{i^0} + {a_{m1}}{i^1} + {a_{m2}}{i^2} + \cdots + {a_{mm}}{i^m} $$ (3) 通过查找Savitzky A.和Golay M.提供的卷积系数表,可以快速确定系数am0, am1, …, amm的值。
S-G算法实现步骤如下:
① 选择移动窗口;②根据移动窗口和拟合阶次拟合曲线;③获取拟合曲线在窗口中心处的值;④根据计算的所有窗口中心值求解多项式系数。
2. 小波变换优化EEMD结合S-G降噪算法
在实际光谱测量中,同时存在高斯白噪声和脉冲噪声。高斯白噪声可以被EEMD有效去除,但同时对于包含有用信息的IMF高频分量也可能被EEMD去除。基于此,可以利用小波阈值法将EEMD分解的各IMF分量进行二次去噪处理,将处理后的各IMF分量进行重构,得到去除噪声后的信号[19]。经小波变换优化后的EEMD可以很好地对高斯白噪声进行去噪,并能保留住原始信号的有效信息,但对于含有脉冲噪声的,其去噪效果没有高斯噪声理想。Savitzky-Golay滤波在脉冲噪声去除上,效果优于小波变换和EEMD。
因此,本文提出一种将小波优化后的EEMD与S-G滤波相结合的红外吸收光谱的滤波方法,从而达到同时去除高斯白噪声和脉冲噪声目的,具体步骤如下:
① 使用EEMD方法对原始信号进行分解,得到多个IMF分量。②对各IMF分量使用小波阈值法进行二次去噪处理。③将去噪后的各IMF分量进行信号重构,得到去噪后信号。④使用S-G方法进行脉冲信号的去除和平滑处理。
3. 实验及仿真验证
3.1 实验设计
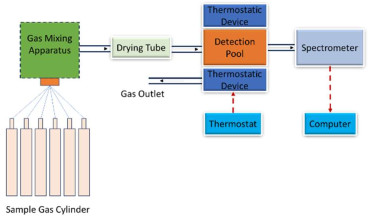
实验装置包括一台傅里叶红外光谱仪、一台混合配气装置、Nafion滤膜式气体干燥管以及一台工控计算机。气体检测池带有保温套及恒温装置。配气装置包含6个样品气进气口、一个氮气稀释进气口和一个出气口,带有氮气清扫功能以及真空抽气泵,实验装置如图 1所示。在实验中,我们以乙烷(C2)为例实验。浓度设置为等梯度递增,如表 1所示。
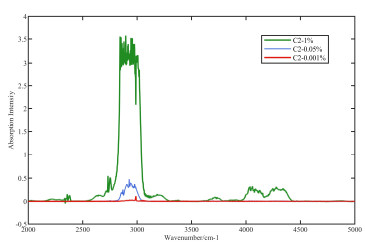
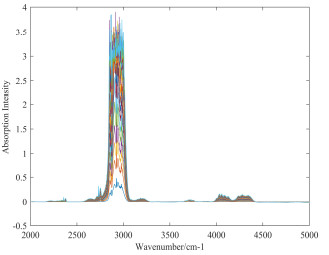
表 1 乙烷实验浓度配置数据Table 1. Ethane experimental concentration configuration dataGas High concentration/(%) Medium concentration/(%) Low concentration/(%) Minimum concentration Gradient Highest concentration Minimum concentration Gradient Highest concentration Minimum concentration Gradient Highest concentration C2 1 5 99.99 0.05 0.05 1 0.001 0.001 0.05 在实验中,我们使用高浓度样品气,按照相应的梯度对实验气体进行配置,共采集41组光谱数据,图 2是乙烷浓度为0.001%、0.05%、1%的吸收光谱图。从图 2可以看出,乙烷的光谱吸收数据含有明显的噪声干扰。本文以1%浓度的乙烷吸收光谱数据为例进行去噪处理,其吸收光谱图,如图 2中的乙烷1%浓度的吸收光谱图所示。
3.2 去噪效果对比分析
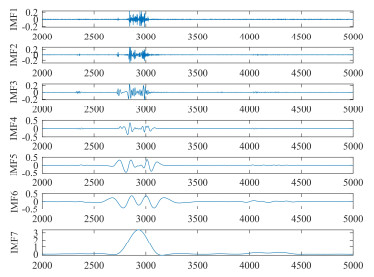
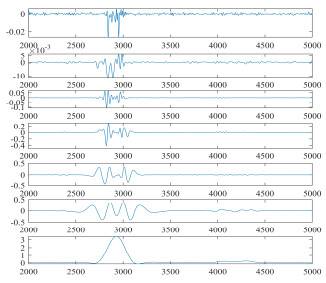
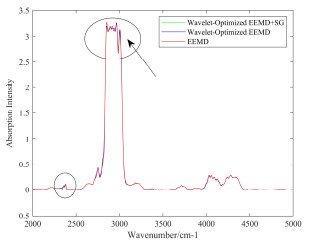
从图 2中乙烷1%浓度的吸收光谱图可以看出,该光谱数据在特征吸收峰附近含有噪声,直接使用它进行定量分析将会得到较差的结果,所以有必要对其进行去噪处理。首先对乙烷吸收光谱数据进行EEMD分解,将标准差和白噪声添加次数设置0.1和200,共得到7个经EEMD分解后的IMF分量,如图 3所示。然后,用小波阈值法对各IMF分量分解去噪,得到结果如图 4所示。将EEMD分解和小波优化后的IMF分量分别进行重构,进一步的,在重构信号的基础上进行Savitzky-Golay去噪处理,共得到3条重构后的信号,如图 5所示。从图 5中两个圈出的位置可以看出,在利用小波优化EEMD分解后的IMF分量重构曲线的基础上进一步使用Savitzky-Golay去噪处理后得到的曲线更加平滑,更可以在图中直观地看出,蓝色的曲线是对红色曲线的去噪,绿色曲线时对蓝色曲线的进一步去噪。在图 5中箭头指向的位置,我们可以知道这是连续吸收光谱不正常的地方,而经过3种去噪方法后,小波优化EEMD加Savitzky-Golay的去噪方法处理结果比其他两种方式更好。
为了更好地对3种去噪方法进行评价,本文采用均方根误差(RMSE)、归一化相关系数(NCC)、信噪比(SNR)3种不同的评价指标对3种去噪方法分别进行比较[20]。计算结果如表 2所示,可以看出,分别从3个指标上来看,都是小波优化EEMD结合SG的去噪方法优于其他两种方法。
表 2 三种去噪方法评价比较Table 2. Comparison of 3 denoising methodsDenoising
methodsEEMD Wavelet+EEMD Wavelet+EEMD
+SGSNR 24.2458 24.3612 24.8464 RMSE 0.79361 0.0448560 0.0447964 NCC 0.99812 0.99817 0.99836 3.3 不同去噪方法对定量分析的影响
为了更好地说明不同去噪方法对定量分析的影响,我们分别使用3种去噪方法对采集的光谱数据集进行处理后,使用基础的PLS算法对乙烷的浓度进行预测。从3.1节设计的实验可以看出,本实验的浓度范围跨度很大,最低浓度为0.001%,最大浓度为100%,如果在全浓度范围内进行预测的话,会导致预测结果较差。为了减少浓度范围对预测结果的准确性,只验证不同去噪方法对定量分析的影响,我们采用中浓度的数据集进行说明,即乙烷浓度为0.05%~1%,而如何在浓度范围跨度大的情况下,达到比较高的预测准确度,我们将在后续的研究中进行说明。
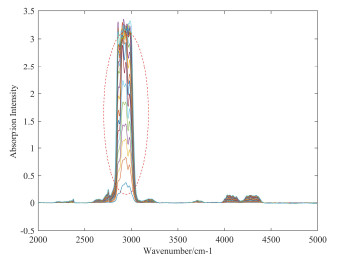
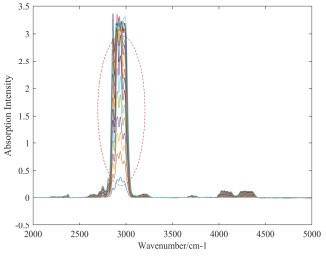
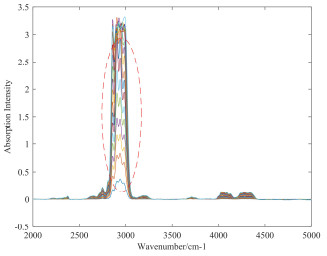
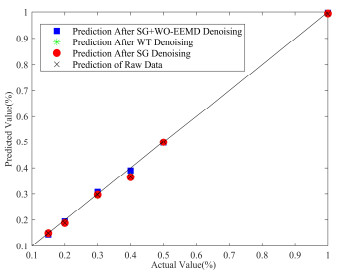
在实验中,我们使用高浓度样品气,按照相应的梯度对实验气体进行配置,采集中浓度样品光谱数据20。首先对采集的所有光谱数据进行不同方法的去噪处理,然后按照7:3的比例随机在中浓度采集的光谱数据中抽取其中的14组作为训练集,其余6组作为测试集对模型进行测试,最后对模型进行训练和预测。采集的原始光谱数据和经不同方法去噪处理后的光谱数据,如图 6~图 9所示。从图 6~图 9可以看出,如3.2节降噪分析所述小波优化EEMD+SG去噪方法对光谱的去噪处理效果要优于其他两种方法。下面是这4种数据集采用PLS方法的浓度预测结果,采用决定系数(R2)和均方根误差(RMSE)2种不同的评价指标对去噪方法分别进行比较,如图 10所示,表 3是这4种预测结果的对比。
表 3 不同去噪方法预测结果比较Table 3. Comparison of prediction results from denoising methodsDenoising
methodsWithout denoising EEMD Wavelet +EEMD Wavelet +EEMD+SG R2 0.9908 0.9909 0.9972 0.9996 RMSE 0.0267 0.0265 0.0146 0.0056 从图 10中,可以看出,采用小波优化EEMD加SG的去噪方法对光谱进行处理后,采用PLS进行预测,得到了预测值与真实值最为接近的结果。从表 3中的对比结果来看,小波+EEMD+SG处理后得到预测结果的相关系数最高,为0.9996,且RMSE值最低,为0.0056。综上,无论从单独去噪结果来看,还是从去噪后的定量分析来看,小波优化EEMD+SG的去噪方法较其他方法更有优势,它能同时去除高斯白噪声和脉冲噪声。
4. 结论
针对录井烃类气体种类多,浓度范围跨度大,尤其当检测浓度范围较小(<500 ppm)时,有效信号容易被噪声淹没,且单一滤波方式在该种情况下去噪能力较差的问题。基于此,本文将小波变换、EEMD和S-G滤波相结合用于吸收光谱数据去噪。该方法集合3者间优势进行互补,实现了能够较好去除浓度范围跨度大的光谱信息中不同噪声的目的。实验表明,通过对乙烷实测吸收光谱数据的去噪分析,该方法能够对光谱数据中的噪声有较好的去除效果,且提高了SNR值,降低了RMSE值。通过去噪结果对比分析,可以得出,该方法在录井气体上的去噪效果优于其他方法。同时,通过使用不同去噪方法处理光谱数据后进行定量分析,定量分析结果表明,使用该去噪方法处理光谱数据后,定量分析预测的结果更加接近真实值。综上,本文所提方法是对录井烃类气体光谱测量一种有效的去噪方法。
-
表 1 乙烷实验浓度配置数据
Table 1 Ethane experimental concentration configuration data
Gas High concentration/(%) Medium concentration/(%) Low concentration/(%) Minimum concentration Gradient Highest concentration Minimum concentration Gradient Highest concentration Minimum concentration Gradient Highest concentration C2 1 5 99.99 0.05 0.05 1 0.001 0.001 0.05 表 2 三种去噪方法评价比较
Table 2 Comparison of 3 denoising methods
Denoising
methodsEEMD Wavelet+EEMD Wavelet+EEMD
+SGSNR 24.2458 24.3612 24.8464 RMSE 0.79361 0.0448560 0.0447964 NCC 0.99812 0.99817 0.99836 表 3 不同去噪方法预测结果比较
Table 3 Comparison of prediction results from denoising methods
Denoising
methodsWithout denoising EEMD Wavelet +EEMD Wavelet +EEMD+SG R2 0.9908 0.9909 0.9972 0.9996 RMSE 0.0267 0.0265 0.0146 0.0056 -
[1] 荆文峰, 阎荣辉, 陈中普, 等. 红外光谱录井技术在长庆油田的创新应用[J]. 录井工程, 2019, 30(3): 124-130. JING Wenfeng, YAN Ronghui, CHEN Zhongpu, et al. Innovative application of infrared spectroscopy logging technology in the Changqing oilfield[J]. Well Logging Engineering, 2019, 30(3): 124-130.
[2] 刘志宏, 邓波, 周玉荣, 等. 红外光谱预处理中去噪的研究[J]. 光谱实验室, 2006(4): 815-819. DOI: 10.3969/j.issn.1004-8138.2006.04.041 LIU Zhihong, DENG Bo, ZHOU Yurong, et al. Research on denoising in infrared spectroscopy preprocessing [J]. Chinese Journal of Spectroscopy Laboratory, 2006(4): 815-819. DOI: 10.3969/j.issn.1004-8138.2006.04.041
[3] 罗方. 基于小波变换的信号去噪研究[J]. 科技风, 2012(16): 67. DOI: 10.19392/j.cnki.1671-7341.2012.16.049. LUO Fang. Research on signal denoising based on wavelet transform[J]. Science and Technology Wind, 2012(16): 67. DOI: 10.19392/j.cnki.1671-7341.2012.16.049.
[4] 王书涛, 曾秋菊, 宋浩兵, 等. 基于SVM滤波器的吸收式甲烷检测的信号去噪方法[J]. 中国激光, 2014, 41(9): 271-275. WANG Shutao, ZENG Qiuju, SONG Haobing, et al. Signal denoising method for absorption-based methane detection using SVM filters[J]. Chinese Journal of Lasers, 2014, 41(9): 271-275.
[5] HUANG N E, ZHENG S, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998: 903-995.
[6] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI: 10.1142/S1793536909000047
[7] 刘铭华. 基于空芯光子带隙光纤的全光纤甲烷检测系统研究[D]. 秦皇岛: 燕山大学, 2015. LIU Minghua. Research on All-Fiber Methane Detection System Based on Hollow-Core Photonic Band Gap Fiber[D]. Qinhuangdao: Yanshan University, 2015.
[8] 王书涛, 车先阁, 王志芳, 等. 基于小波优化EEMD的甲烷浓度检测信号研究[J]. 光学技术, 2019, 45(3): 269-274. WANG Shutao, CHE Xiange, WANG Zhifang, et al. Study on methane concentration detection signals based on wavelet-optimized EEMD[J]. Optical Techniques, 2019, 45(3): 269-274.
[9] 秦亚辉, 冯景辉, 陈立定. 基于小波变换的信号去噪方法研究[J]. 信息技术, 2010, 34(1): 53-57. QIN Yahui, FENG Jinghui, CHEN Liding. Study on signal denoising methods based on wavelet transform [J]. Information Technology, 2010, 34(1): 53-57.
[10] 郭飞, 王玉兰. 小波变换与匹配滤波耦合的激光雷达弱信号处理[J]. 激光杂志, 2006(4): 51-52. GUO Fei, WANG Yulan. Weak signal processing of Lidar based on coupling of wavelet transform and matched filtering [J]. Laser Journal, 2006(4): 51-52.
[11] 秦瑞霞, 黄毅. 基于阈值函数的小波去噪的研究[J]. 信息通信, 2016(12): 1-3. QIN Ruixia, HUANG Yi. Research on wavelet denoising based on threshold function[J]. Information Communication, 2016(12): 1-3.
[12] 赵肖宇. 基于EMD和EEMD的自适应光谱预处理方法及其应用研究[D]. 秦皇岛: 燕山大学, 2015. ZHAO Xiaoyu. Adaptive Spectral Preprocessing Methods Based on EMD and EEMD and Their Applications[D]. Qinhuangdao: Yanshan University, 2015.
[13] ZHOU Y, TAO T, MEI X, et al. Feed-axis gearbox condition monitoring using built-in position sensors and EEMD method[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(4): 785-793 http://www.xueshufan.com/publication/2052675069
[14] 王玉静, 康守强, 张云, 等. 基于集合经验模态分解敏感固有模态函数选择算法的滚动轴承状态识别方法[J]. 电子与信息学报, 2014, 36(3): 595-600. WANG Yujing, KANG Shouqiang, ZHANG Yun, et al. Rolling bearing condition recognition method based on sensitive intrinsic mode function selection algorithm using ensemble empirical mode decomposition [J]. Journal of Electronics & Information Technology, 2014, 36(3): 595-600.
[15] 杨帆, 王鹏, 张宁超, 等. 一种基于小波变换的改进滤波算法及其在光谱去噪方面的应用[J]. 国外电子测量技术, 2020, 39(8): 98-104. YANG Fan, WANG Peng, ZHANG Ningchao, et al. An improved filtering algorithm based on wavelet transform and its application in spectral denoising [J]. Foreign Electronic Measurement Technology, 2020, 39(8): 98-104.
[16] 李亢, 杨绍清. 基于Savitzky-Golay算法的图像平滑去噪[J]. 数据采集与处理, 2010, 25(S1): 72-74. LI Kang, YANG Shaoqing. Image smoothing and denoising based on the Savitzky-Golay algorithm[J]. Data Acquisition and Processing, 2010, 25(S1): 72-74.
[17] 雷林平. 基于Savitzky-Golay算法的曲线平滑去噪[J]. 电脑与信息技术, 2014, 22(5): 30-31. LEI Linping. Curve smoothing and denoising based on the Savitzky-Golay algorithm [J]. Computer and Information Technology, 2014, 22(5): 30-31.
[18] 蔡天净, 唐瀚. Savitzky-Golay平滑滤波器的最小二乘拟合原理综述[J]. 数字通信, 2011, 38(1): 63-68, 82. CAI Tianjing, TANG Han. A review of the least squares fitting principle of the Savitzky-Golay smoothing filter[J]. Digital Communication, 2011, 38(1): 63-68, 82.
[19] 张林, 张志杰, 张华. 小波变换在压力传感器输出信号去噪中的应用[J]. 仪表技术与传感器, 2018(4): 10-13. ZHANG Lin, ZHANG Zhijie, ZHANG Hua. Application of wavelet transform in denoising of pressure sensor output signals [J]. Instrument Technology and Sensors, 2018(4): 10-13.
[20] 王志芳, 王书涛, 王贵川, 等. 基于小波优化EEMD的二氧化硫检测[J]. 计量学报, 2020, 41(6): 752-758. WANG Zhifang, WANG Shutao, WANG Guichuan, et al. Sulfur dioxide detection based on wavelet-optimized EEMD[J]. Acta Metrologica Sinica, 2020, 41(6): 752-758.



 下载:
下载: