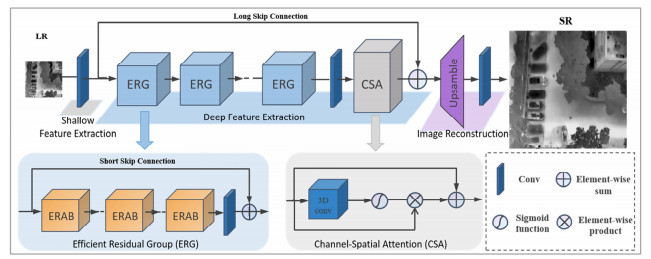
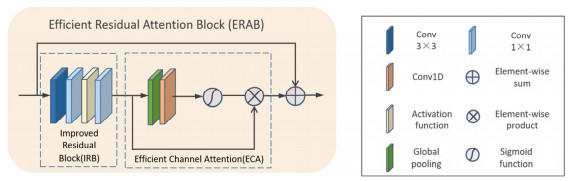
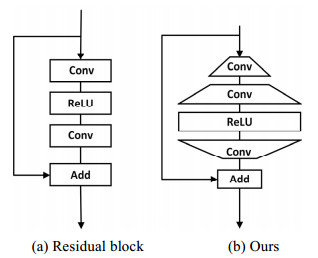
Infrared Images with Super-resolution Based on Deep Convolutional Neural Network
-
摘要: 由于器件及工艺等技术限制,红外图像分辨率相对可见光图像较低,存在细节纹理特征模糊等不足。对此,本文提出一种基于深度卷积神经网络(convolutional neural network,CNN)的红外图像超分辨率重建方法。该方法改进残差模块,降低激活函数对信息流影响的同时加深网络,充分利用低分辨率红外图像的原始信息。结合高效通道注意力机制和通道-空间注意力模块,使重建过程中有选择性地捕获更多特征信息,有利于对红外图像高频细节更准确地进行重建。实验结果表明,本文方法重建红外图像峰值信噪比(peak signal to noise ratio,PSNR)优于传统的Bicubic插值法以及基于CNN的SRResNet、EDSR、RCAN模型。当尺度因子为×2和×4时,重建图像的平均PSNR值比传统Bicubic插值法分别提高了4.57 dB和3.37 dB。Abstract: Owing to technical limitations regarding the device and process, the resolution of infrared images is relatively low compared to that of visible images, and deficiencies occur such as blurred textural features. In this study, we proposed a super-resolution reconstruction method based on a deep convolutional neural network (CNN) for infrared images. The method improves the residual module, reduces the influence of the activation function on the information flow while deepening the network, and makes full use of the original information of low-resolution infrared images. Combined with an efficient channel attention mechanism and channel-space attention module, the reconstruction process selectively captures more feature information and facilitates a more accurate reconstruction of the high-frequency details of infrared images. The experimental results show that the peak signal-to-noise ratio (PSNR) of the infrared images reconstructed using this method outperforms those of the traditional Bicubic interpolation method, as well as the CNN-based SRResNet, EDSR, and RCAN models. When the scale factor is ×2 and ×4, the average PSNR values of the reconstructed images improved by 4.57 and 3.37 dB, respectively, compared with the traditional Bicubic interpolation method.
-
0. 引言
随着红外成像技术的进步,其广泛应用于军事与民用领域[1],由于红外图像成像是根据物体自身散发热辐射多少的差异区分出不同的物体,最终将差异转换为人眼可见的图像,生成的红外图像属于灰度图像,不具有可见光图像的色彩区分度,再加之环境温度、大气衰减等的影响,最终输出的红外图像成像的品质较差[2],分辨率较低,并且普遍存在着对比度低、图像边缘模糊、细节信息少等缺陷,由于设备的限制和外界环境多种因素的影响,导致红外图像产生了多种多样的噪声[3],使得生成的红外图像的信噪比较低,对人眼的观察目标造成很大的不便。红外图像降噪算法如何在降低红外图像噪声的同时,尽可能多的保留细节信息,是需要深入研究的问题。
红外图像降噪处理是红外成像技术中重要的组成部分[4],为满足不同领域特别是军用领域的要求,对红外图像进行更高性能和更高效率的降噪处理已经成为一种趋势。传统的红外图像降噪算法大体上可分为空间域降噪算法与变换域降噪算法,空间域降噪算法主要包括高斯滤波、中值滤波和均值滤波等方法,降噪效果与对细节信息的保留不足;变换域降噪算法主要包括小波变换、Contourlet变换等方法,对细节信息的保留效果较好,但是算法复杂度偏高,难以满足实时性的要求。近年来,基于图像分层[5]的降噪算法得到了科研人员的重视,通过低通滤波器将红外图像进行平滑处理,作为背景层,再通过输入红外图像与背景层作差,得到细节层。对含有细节信息包括噪声的细节层进行降噪处理,将处理后的细节层与背景层合并还原,输出图像。常用的滤波器有引导滤波、双边滤波、加权最小二乘滤波等。
由于红外图像噪声有很多种类型,其生成过程随机且复杂,包含很多不精确的信息,粗糙集理论[6]是一种处理不确定信息的理论,能够将不确定、不精确的信息进行分类。本文针对红外图像在降噪的同时,尽可能的兼顾细节保留与实时性的问题,将粗糙集引入红外图像的降噪处理中[7],并根据红外图像的灰度分布,基于红外图像分层处理的思想,通过引导滤波对红外图像进行分层,再引入粗糙集理论对红外图像细节层进行进一步的分层降噪处理,提出了一种基于粗糙集的红外图像多维降噪方法。
文献[8]将粗糙集理论结合中值滤波应用于红外图像处理,阐明了粗糙集理论应用于红外图像处理的可行性,对于红外图像的边缘信息有较好的保留效果,并且说明了对于噪声分类处理的效果良好。
文献[9]结合粗糙集理论与小波变换理论,提出了一种新的结合红外图像降噪方法。将经过降噪处理后的子图进行通过小波变换,最终得到处理后的红外图像。在具有良好降噪效果的同时能够对红外图像边缘及细节信息进行小幅度的增强,但是仍会存在一定的细节丢失状况,需要进一步研究和改进。
文献[10]通过将直方图均衡以及粗糙集理论相互结合的方式,使得红外图像的边缘信息更加清晰,提升红外图像的对比度,以达到更好的红外图像处理效果。证明了此算法具有较高的有效性以及可行性。
通过粗糙集理论与其他降噪算法相结合的方式,对于抑制红外图像噪声有较好的效果,但是仍然存在小细节丢失的情况,具有更深入的研究空间。
1. 本文算法
本文使用探测器采集的原始14 bits红外图像作为输入图像,图像尺寸为1024×768,算法框图如图 1所示,输入红外图像通过引导滤波得到背景层与细节层,再运用粗糙集理论对细节层进一步地分层,经过噪声抑制与细节增强,与背景层合并,最后输出处理后的8 bits红外图像。
1.1 引导滤波
引导滤波[11]属于线性变换滤波的一种,通过一张导引图,对输入图像进行对比滤波处理,使得最后的输出图像接近于输入图像,属于边缘保持的平滑滤波,对于红外图像的分层处理起到了关键的作用[12]。引导滤波能在平滑图像的同时对红外图像边界保持可以起到较好的作用。引导滤波的数学模型如表 1:
$$ {Q_i} = {\bar a_i}{I_i} + {b_i}, \quad \forall i \in {w_k} $$ (1) $$ {\bar a_i} = \frac{1}{{\left| w \right|}}\sum\limits_{k:i \in {w_k}} {{a_k}} $$ (2) $$ {a_k} = \frac{{\frac{1}{{\left| w \right|}}\sum\limits_{i \in {w_k}} {{I_i}{P_i} - {\mu _k}{{\bar p}_k}} }}{{\sigma _k^2 + \varepsilon }} $$ (3) $$ {\bar b_i} = \frac{1}{{\left| w \right|}}\sum\limits_{k:i \in {w_k}} {{b_k}} $$ (4) $$ {b_k} = {\bar P_k} - {a_k}{\mu _k} $$ (5) 表 1 不同算法降噪效果客观评价指标Table 1. Objective evaluation index of noise reduction effect of different algorithmsAlgorithm Peak Signal To Noise Ratio(PSNR) Entropy Guided filtering 54.5211 6.1239 Bilateral filtering 55.3598 6.1274 Least square filtering 57.7474 6.3115 The algorithm in this paper 58.7371 6.4126 式中:Qi为输出图像;Ii为引导图像;Pi表示输入图像;i表示位置像素点;wk表示确定的窗口;${\bar a_i} $和$ {\bar b_i}$建立了每个像素点从输入到输出的关系;ak和bk是唯一确定的常量系数;|w|表示窗口内像素点的个数;μk和σk2分别表示窗口wk内的平均值和方差; $ {\bar P_k}$是输入图像在窗口wk中的平均值。ε为正则化参数,用于避免ak过大。
1.2 粗糙集理论
红外图像的各种降噪算法有不同的优点和缺点[13],但是由于数字图像数据量大、噪声种类复杂以及场景的变化等因素,使得在实际的应用中,会出现很多问题。由于图像本身信息的复杂性和信息之间较强的相关性,在处理过程中可能出现不完整性和不精确性等问题,将粗糙集应用于红外图像的处理,可以将这些信息重新进行分类整合,有助于红外图像的质量提升。
粗糙集理论将一幅M×N个像素的红外图像看作一个整体系统,红外图像中的每个像素为系统中的一个对象。
设一个3×3的模板,将以中心点为核心的4个2×2的子模板划分为4个方向。如图 2、3所示。
通过计算模板中心像素与周围模板像素灰度均值差的统计特征来定义子模板中的等价关系。
设F(i, j)为窗口中心像素的灰度值,第k(k=1, 2, 3, 4)个模板去掉中心像素外的其它像素灰度值和为Fk,则中心像素与第k个模板的灰度差异为D(k),其表达式如下:
$$ D\left( k \right) = \left| {\frac{1}{3}\left[ {F\left( {i, j} \right) \times 3 - {F_k}} \right]} \right| $$ (6) 则模板中心像素与周围模板灰度差异均值为:
$$ {\rm{Mean}}(i, j) = \frac{1}{4}\sum\limits_{k = 1}^4 {D\left( k \right)} $$ (7) 模板中心像素与周围模板灰度差异方差为:
$$ {\rm{Var}}\left( {i, j} \right) = \frac{1}{4}\sum\limits_{k = 1}^4 {{{\left[ {D\left( k \right) - {\rm{Mean}}\left( {i, j} \right)} \right]}^2}} $$ (8) 定义如下两个等价关系:
1)等价关系Eq1:中心像素与其相邻模板间灰度均值大于阈值The_Mean,则Eq1表示与周围模板灰度差异均值较大的像素。
2)等价关系Eq2:中心像素与其相邻模板灰度方差小于等于阈值The_Var,则Eq2表示与周围模板灰度差异方差较小的像素。
显然,噪声像素点与相邻模板灰度均值差异较大且与相邻模板灰度差异方差较小。这里The_Mean与The_Var取两者最大值的一半作为阈值。
用X表示噪声像素集合,则X的上、下近似如下:
$$ {E_{\rm{d}}}\left( X \right)=E{{\rm{q}}_1} \cap E{{\rm{q}}_2} $$ (9) $$ {E_{\rm{u}}}\left( X \right)=E{{\rm{q}}_1} \cup E{{\rm{q}}_2} $$ (10) $$ {P_1}={E_{\rm{d}}}\left( X \right) $$ (11) $$ {P_2}={E_{\rm{u}}}\left( X \right) - {E_{\rm{d}}}\left( X \right) $$ (12) $$ {P_3}=I - {P_2} - {P_1} $$ (13) 式中:Ed(X)表示所有确定含噪声像素的集合;Eu(X)表示所有可能含噪声像素的集合;P1、P2、P3分别为确定含噪声子图、可能含噪声也可能不含噪声子图及确定不含噪声子图;P1、P2即为需要噪声抑制的子图。
以上为应用粗糙集理论对采集到的红外图像进行子图的划分,将含有不同信息的子图进行分类。再对含有不同信息的子图分别进行处理,最后将处理后的子图进行合并还原为细节层,再与背景层合并,最终输出红外图像。
1.3 多维噪声自适应降噪系数
在图像细节多的区域,图像的局部方差大,噪声可能被细节所掩盖[14],而在图像细节少的区域,噪声易于观察到。在对细节层图像进行降噪时,图像的细节降噪系数根据图像的不同区域自适应地进行变化,降噪系数公式如下所示:
$$ v\left( {i, j} \right) = \frac{1}{{m\left( {i, j} \right)*\omega + 1}} $$ (14) $$ g\left( {i, j} \right) = {g_{\rm{L}}} + \left[ {1 - v\left( {i, j} \right)} \right]*\left( {{g_{\rm{H}}} - {g_{\rm{L}}}} \right) $$ (15) 式中:定义噪声掩膜函数m(i, j)与图像的局部方差有关;v(i, j)用于表征噪声可见性与掩膜函数之间的关系;gL为图像低增益值;gH为图像高增益值,在统计图像中的某个像素点v(i, j)趋近于零时,该像素点的降噪系数取值相对较大,反之系数取值相对较小。为了不使图像的细节层信息被过多的抑制,gL与gH的选值为较小的整数。
1.4 多维降噪算法
通过引导滤波将输入图像分为背景层与细节层后,将细节层通过粗糙集理论进行进一步的分层处理,将细节层子图划分为低噪声子图、不确定含噪声子图与高噪声子图 3个子图层。由于目前红外图像还达不到无噪处理,将含有较多细节信息的子图称为低噪子图。将算法分离出的多数噪声与细节信息共存的子图称为不确定含噪声子图,将算法确定分离出的多数为噪声的子图称为高噪声子图。
对于分层的3个子图,分别进行不同的增强与抑制,最后将子图相加合并还原出处理后的图像。合并公式如下所示:
$$ S = a \times {I_1} + b \times {I_2} + c \times {I_3} $$ (16) $$ P = S + {\rm{Back}} $$ (17) 式中:P为最终输出图像;S为合并还原的图像;Back为引导滤波分离出的背景层。I1、I2、I3分别为经过粗糙集多维分层处理的低噪声子图、不确定含噪声子图与高噪声子图;a、b、c分别为子图的增益系数,对于低噪声子图,设置增益系数a,对子图细节进行增强,通常情况下a>1。经过仿真实验选取a=1.5效果良好。对于不确定噪声子图,设置自适应降噪系数b,对子图细节进行自适应增强,取b=g(i, j)。对于高噪声子图,设置增益系数c,对子图细节进行增强,通常情况下c<1。经过仿真实验选取c=0.6效果良好。
通过选取增益系数与自适应降噪系数,对红外图像经过多维分层的子图分别用不同的系数进行处理,对噪声更多的子图进行抑制,对细节更多的子图进行增强,对不确定噪声子图进行自适应降噪,最终达到噪声抑制兼顾细节增强的良好效果。
2. 仿真实验结果及分析
红外探测器采集到的原始图像是14 bits或者更高位的灰度图像,一般而言,人眼对于灰度的分辨极限还无法达到目前显示设备的8 bits,更无法达到红外探测器采集到的14位或者更高位数的图像。需要对探测器采集到的原始图像进行动态压缩,将红外图像从14 bits压缩到人眼能够观察的8 bits。原始输入红外图像分辨率为1024×768,位深为14 bits。如图 4为经过引导滤波分层的图像,背景层经过直方图动态压缩,细节层由于数值较小,不需要压缩可以直接显示出来。
运用粗糙集理论将细节层进一步细分为3个子图,进行多维度的分层,如图 5所示,分别对3个子图进行噪声抑制与细节增强处理,处理后将子图合并,得到处理后的细节层。
将处理后的细节层与背景层合并,最终的到处理后的输出红外图像,如图 6所示。将未经处理的细节层与经过动态压缩的背景层合并,得到经过压缩与引导滤波分层但是未经降噪处理的8 bits原始图像,作为降噪处理前后对比的输入图像。
为了更好地验证粗糙集红外图像多维分层降噪算法的处理效果,选用较为干净的8 bits红外图像,对其添加条纹噪声,通过对比其他算法效果侧面体现出本文的降噪算法处理效果。
如图 6所示,从不同算法对比图看,经过引导滤波自适应增益系数中值滤波分层处理得到的细节层含有较多的条纹噪声,对于条纹噪声的抑制效果并不明显,物体边缘以及弱小目标的细节部分有一定的增强效果,整体处理后的图像有一定程度的损失。经过双边滤波自适应增益系数中值滤波处理后的细节层对于条纹噪声有着一定的降噪效果,细节部分得到了一定的增强,但是算法复杂度高,缺乏实时性,难以实现工程化。加权最小二乘滤波自适应增益系数中值滤波对条纹噪声有一定的抑制效果,但是对于细节增强效果并不算理想,且算法复杂度相对引导滤波较高。本文算法在保证降噪效果的同时对图像中的细节信息与图像边缘信息有较好的增强效果,对复杂背景下的细节信息以及边缘保留较好,空旷背景下噪声抑制效果较好,且实时性好,满足工程化应用的需求。
另外采用峰值信噪比、信息熵两种客观评价指标对不同算法进行了客观评价,如表 1所示。从结果可得,本文算法的峰值信噪比高于其他算法处理图像,信息熵值高于对其他算法处理后的红外图像,峰值信噪比越高说明噪声抑制的效果越好,信息熵值越大表明图像信息量越多,从客观评价指标说明了本文算法对红外图像的噪声具有较好的抑制效果,并且对细节部分有一定幅度的增强效果。
另外,本文还对不同算法的运行时间,分别通过Matlab进行对比仿真,仿真平台:Lenovo系列笔记本电脑,CPU:AMD Ryzen7 4800H @2.9GHz16GB内存,计算环境:Matlab\R2018b。结果如表 2所示。通过分析表 2的数据,引导滤波的时间复杂度为O(N),N为图像像素总数,与滤波半径无关,复杂度较低。双边滤波的时间复杂度为O(σ2),其中σ为高斯核函数的标准差,时间复杂度较高。加权最小二乘的时间复杂度为O(mN),其中N为图像像素总数,m为常数系数,时间复杂度较高。本文改进算法的时间复杂度为O(N),即在传统引导滤波的基础上结合本文算法,可以更高效地对图像进行处理,具有时间复杂度上的优势。在图像分辨率越来越高,图像像素越来越多的当下,具有时间复杂度优势的算法更具有实际应用价值。
表 2 不同算法运行时间对比Table 2. Running time comparison of different algorithmsAlgorithm Time complexity Running time/s Guided filtering O(N) 2.744 Bilateral filtering O(σ2) 5.273 Least square filtering O(mN) 4.397 The algorithm in this paper O(N) 3.174 本文算法和上述改进的自适应双边滤波与自适应加权最小二乘滤波算法的运行时间相比,算法运行时间低得多。略大于改进的自适应引导滤波运行时间,红外图像的处理效果优于自适应引导滤波。综合来看,本文提出的基于粗糙集的红外图像多维降噪算法具有一定的实时处理应用价值。
3. 结论
针对高位深度的红外图像噪声抑制以及兼顾细节增强问题,本文结合引导滤波和粗糙集理论,提出了一种基于粗糙集的红外图像多维分层的降噪算法。通过对几个不同场景下红外图像降噪算法处理效果的对比仿真,从降噪图像的主观感受与客观评价指标来看,可以发现本文算法能够很好地抑制横竖条纹噪声,具有较好的保边性与降噪效果,同时对于红外图像中细节信息的增强,具有较好的效果,算法复杂度低,实时性高,具有一定的实际应用价值,在细节层细节保留方面以及背景层动态压缩方面还有研究改进的空间,还需要深入地研究与改进。
-
表 1 ERAB(包括IRB和ECA)和CSA的研究
Table 1 Investigations of ERAB (including IRB and ECA) and CSA
Base M1 M2 M3 M4 IRB √ √ √ √ CSA √ √ ECA √ √ PSNR/dB 42.44 42.78 42.97 42.86 43.06 SSIM 0.9543 0.9549 0.9552 0.9550 0.9554 表 2 典型图像实验结果对比
Table 2 Comparison of typical images experiment results
Images Scale Bicubic
(PSNR/dB)/SSIMSRResNet
(PSNR/dB)/SSIMEDSR
(PSNR/dB)/SSIMRCAN
(PSNR/dB)/SSIMOurs
(PSNR/dB)/SSIMTEST_1 ×2 38.0631/0.9710 43.0650/0.9868 43.1183/0.9869 43.1627/0.9870 43.3488/0.9875 TEST_2 30.8528/0.7505 32.1850/0.7875 32.1907/0.7878 32.1908/0.7880 32.2152/0.7881 TEST_3 ×4 31.8568/0.9091 35.4462/0.9498 35.3748/0.9493 35.7971/0.9516 36.0539/0.9538 TEST_4 28.6532/0.8888 35.3544/0.9551 35.3770/0.9548 35.5273/0.9559 36.1061/0.9586 表 3 测试图像集超分辨率重建结果比较
Table 3 Comparison of super-resolution reconstruction results of test image set
Methods (PSNR/dB)/SSIM(×2) (PSNR/dB)/SSIM(×4) Bicubic 38.4937/0.9395 32.3882/0.8699 SRResNet 41.6272/0.9220 34.8284/0.8999 EDSR 41.6705/0.9221 35.4601/0.9035 RCAN 42.5441/0.9546 35.5871/0.9042 OURS 43.0616/0.9554 35.7599/0.9053 -
[1] Baker S, Kanade T. Limits on super resolution and how to break them[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 24(9): 1167-1183. http://www.onacademic.com/detail/journal_1000035551419310_c5fb.html
[2] Hou H, Andrews H. Cubic splines for image interpolation and digital filtering[J]. IEEE Transactions on acoustics, speech, and signal processing, 1978, 26(6): 508-517. DOI: 10.1109/TASSP.1978.1163154
[3] Freeman W T, Pasztor E C, Carmichael O T. Learning low-level vision[J]. International Journal of Computer Vision, 2000, 40(1): 25-47. DOI: 10.1023/A:1026501619075
[4] YANG J, Wright J, HUANG T S, et al. Image super-resolution via sparse representation[J]. IEEE transactions on image processing, 2010, 19(11): 2861-2873. DOI: 10.1109/TIP.2010.2050625
[5] DONG C, Loy C C, HE K, et al. Image super-resolution using deep convolutional networks[J]. IEEE Trans Pattern Anal Mach Intell, 2016, 38(2): 295-307. DOI: 10.1109/TPAMI.2015.2439281
[6] DONG C, Loy C C, TANG X. Accelerating the super-resolution convolutional neural network[C]//Proceedings of the European conference on computer vision (ECCV), 2016: 391-407.
[7] SHI W, Caballero J, Huszár F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2016: 1874-1883.
[8] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 770-778.
[9] Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017: 4681-4690.
[10] Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2017: 136-144.
[11] ZHANG Y, LI K, LI K, et al. Image super-resolution using very deep residual channel attention networks[C]//Proceedings of the European Conference on Computer Vision (ECCV), 2018: 286-301.
[12] DAI T, CAI J, ZHANG Y, et al. Second-order attention network for single image super-resolution[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019: 11065-11074.
[13] NIU B, WEN W, REN W, et al. Single image super-resolution via a holistic attention network[C]//Proceedings of the European Conference on Computer Vision (ECCV), 2020: 191-207.
[14] Choi Y, Kim N, Hwang S, et al. Thermal image enhancement using convolutional neural network[C]//2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). 2016: 223-230.
[15] HE Z, TANG S, YANG J, et al. Cascaded deep networks with multiple receptive fields for infrared image super-resolution[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2018, 29(8): 2310-2322. http://www.xueshufan.com/publication/2886209123
[16] ZOU Y, ZHANG L, LIU C, et al. Super-resolution reconstruction of infrared images based on a convolutional neural network with skip connections[J]. Optics and Lasers in Engineering, 2021, 146: 106717. DOI: 10.1016/j.optlaseng.2021.106717
[17] YU J, FAN Y, YANG J, et al. Wide activation for efficient and accurate image super-resolution[J/OL]. arXiv preprint arXiv: 1808.08718, 2018.
[18] WANG Q, WU B, ZHU P, et al. ECA-Net: Efficient channel attention for deep convolutional neural networks[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020: 11534-11542.
-
期刊类型引用(1)
1. 王锦荣,叶建春,侯丽英,吴双娥,米成栋. 基于Zemax非球面单透镜的优化设计. 空间电子技术. 2024(05): 87-92 .  百度学术
百度学术
其他类型引用(1)




 下载:
下载: