False Alarm Rate Reduction in Infrared Search and Track Systems
-
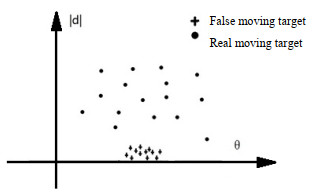
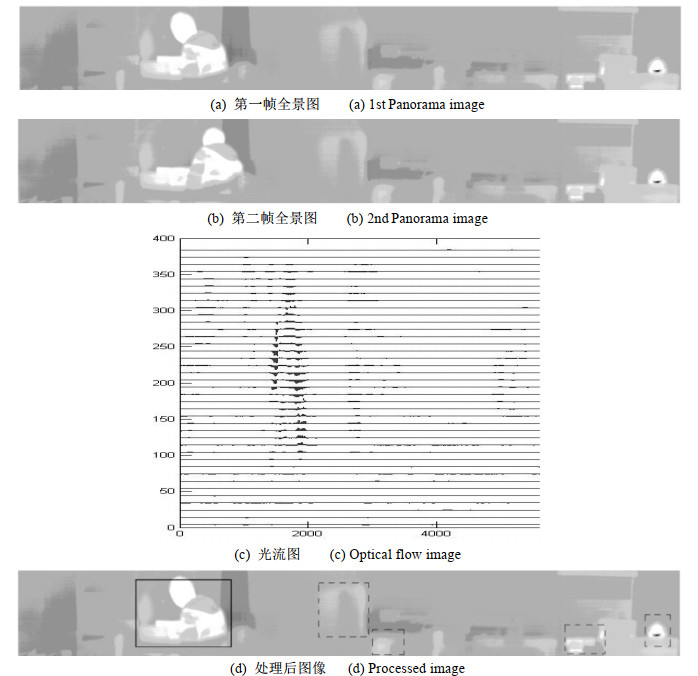
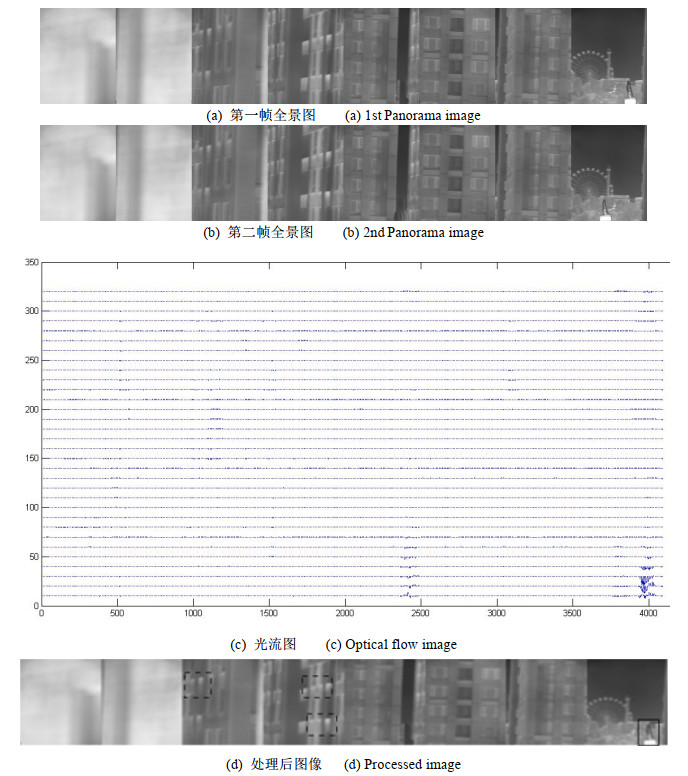
摘要: 红外全景搜索跟踪系统能对360°大视场提供实时多目标搜索与定位功能，与此同时大视场的引入也带来虚假目标增多，以及同一运动目标在前后生成的两幅全景图像中位置差异过大的困扰。本文针对以上问题，引入图像金字塔变换降低全景图像分辨率，再利用Lucas-Kanade（LK）光流法计算所有疑似运动区域的光流，最后分析所有光流特征结合二分类思想将真实运动目标和虚假运动目标区分开，针对全景图像能够有效的将虚假目标检测出来，剔除该类目标对后续处理结果的干扰。
-
关键词:
- 全景搜索跟踪 /
- 虚警率 /
- Lucas-Kanade光流 /
- 二分类
Abstract: Infrared panoramic search and track systems can provide real-time multi-target search and positioning functions for a 360° field of view. However, the involvement of the large view field introduces problems such as increased number of false targets and a large displacement of moving targets between panoramic frames. To address these problems, this study uses the image pyramid transform to reduce the panoramic image resolution and the Lucas-Kanade optical-flow method to calculate the optical flow of all predicted movement areas. Finally, the optical-flow features are analyzed to separate the real target from the false target area. In this way, false targets can be effectively detected in the panorama images, and the interference of such targets in the subsequent processing can be eliminated.-
Keywords:
- panoramic search and track /
- false alarm rate /
- Lucas-Kanade optical-flow /
- dichotomy
-
0. 引言
侦察车辆通常装备有集成高清CCD摄像机、红外热像仪的光电云台，以便于昼夜实时获取侦察车辆周边态势。为了减少观察盲区，获取更远范围的视场，通常将光电云台置于升降式桅杆顶端。受限于重量、成本和技术限制，升降式桅杆一般都为空心结构，这导致桅杆结构刚度明显低于车辆安装基面。光电云台安装于桅杆顶端后，云台方位向的加减速切换以及不同的速度控制方式易使桅杆产生挠曲变形[1]，载体车辆发动机的振动也会传递到桅杆上，这将加剧桅杆振动，导致光电云台视场模糊，严重时甚至导致光电云台转动异常。
通过对光电云台共振原因进行分析，结合观测到的光电云台共振时的速度时域波形，对升降式光电云台的共振现象有了进一步认识。为了解决这一问题，文中分别采用了速度环添加巴特沃斯低通滤波器、速度环添加陷波滤波器、速度环采用自抗扰控制方式来抑制共振。实验结果表明采用自抗扰控制方式可以实现在无需降低光电云台动态性能的前提下，仍能具有良好的共振抑制效果。
1. 共振原理分析
光电云台安装于倒伏升降式桅杆顶部，倒伏升降式桅杆基座安装于车辆载体表面，系统安装连接关系示意图如图 1所示。
云台方位电机采用了正弦波永磁同步电机，由于云台重心与桅杆轴向不一定完全重合以及桅杆自身结构刚度不足，当云台方位向转动时，桅杆会不可避免地产生柔性形变，此时可将桅杆和光电云台统一视为一个二质量柔性伺服系统进行分析[2]，该简化模型如图 2所示。
电机和负载侧动力学方程：
$$ \left\{ \begin{array}{l} {J_{\rm{M}}}\frac{{{\text{d}}{\omega _1}}}{{{\rm{d}}t}} = {T_{\rm{e}}} - {f_1}{\omega _1} - {T_{\text{s}}} \\ {J_{\rm{L}}}\frac{{{\rm{d}}{\omega _2}}}{{{\rm{d}}t}} = {T_{\rm{s}}} - {f_2}{\omega _2} - {T_{\rm{L}}} \\ {\omega _1} = \mathop {{\theta _1}}\limits^ {\bullet} \\ {\omega _2} = \mathop {{\theta _2}}\limits^ {\bullet} \\ {\theta _{\text{s}}} = {\theta _1} - {\theta _2} \\ {T_{\text{s}}} = {f_{\text{s}}}\frac{{{\text{d}}{\theta _{{s}}}}}{{{\rm{d}}t}} + {K_{\rm{s}}}{\theta _{\text{s}}} \end{array} \right. $$ (1) 式中：Te为电机输出转矩；Ts为连接轴转矩；TL为负载扰动转矩；JM为电机惯量；JL为负载惯量；θ1为电机转角；θs为连接轴转角；θ2为负载转角；ω1为电机转速；ω2为负载转速；f1为电机阻尼系数；fs为连接轴阻尼系数；f2为负载阻尼系数；Ks为连接轴刚度系数。
忽略电机、负载的阻尼系数以及负载的扰动转矩影响，由式(1)可得到负载转速和电机转矩的传递函数为：
$$ \frac{{{\omega _{\text{2}}}}}{{{T_{\text{e}}}}} = \frac{{{f_{\rm{s}}}s + {K_{\rm{s}}}}}{{{J_{\rm{M}}}{J_{\rm{L}}}{s^3} + ({J_{\rm{M}}} + {J_{\rm{L}}})({f_{\rm{s}}}s + {K_{\rm{s}}})s}} $$ (2) 由式(2)可知系统零点存在一组谐振频率${\omega _{\text{z}}} = \sqrt {\frac{{{K_{\rm{s}}}}}{{{f_{\rm{s}}}}}} $使系统产生共振，极点存在一组反谐振频率$ {\omega }_{\text{p}}=\sqrt{\frac{{K}_{{\rm{s}}}({J}_{{\rm{M}}}+{J}_{{\rm{L}}})}{{J}_{{\rm{M}}}{J}_{{\rm{L}}}}} $使系统不响应任何输入。一旦有相应频率的激励信号，系统在这两个频率点将易发生机械共振[3]。
2. 共振抑制方式介绍
2.1 速度环添加巴特沃斯滤波器
巴特沃斯滤波器在相同阶数的滤波器中，具有最大斜率的衰减，且在波特图幅频特性中不产生凸峰，因此在控制系统中被经常采用[4]。文中采用阻尼比为0.707的二阶巴特沃斯低通滤波器为：
$$ {G_{\text{b}}}(s) = \frac{{\omega _{\text{n}}^2}}{{{s^2} + \sqrt 2 {\omega _{\rm{n}}}s + \omega _{\rm{n}}^2}} $$ (3) 将巴特沃斯滤波器添加到速度环中，用于对采用M法（即通过在固定时间间隔获得的转角差值求商）取得的电机转速进行滤波，如图 3所示。
2.2 速度环添加陷波滤波器
陷波滤波器是一种带阻滤波器，它可将陷波中心频率附近的频率点的输入幅值衰减到对系统的影响最小，而对陷波频带以外的频率信号基本没有影响[5]。因此是一种得到广泛应用的机械共振抑制方法。一种常用的陷波滤波器传递函数表达式为：
$$ \left\{ {\begin{array}{*{20}{l}} {{G_x}(s) = \frac{{a{s^2} + cs + 1}}{{a{s^2} + bs + 1}}} \\ {a = \frac{1}{{\omega _{{n}}^2}}\mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} } \\ {b = {B_\omega }a\mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} } \\ {c = b \cdot {{10}^{(\frac{{{D_\omega }}}{{20}})}}\mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} } \end{array}} \right. $$ (4) 式中：ωn为陷波频率；Bω为陷波滤波器的陷波带宽；Dω为陷波滤波器的陷波深度。
ωn的值应根据系统共振频率进行调整，以使得陷波滤波器可以将共振频率抑制住；通过调整陷波带宽Bω值和陷波滤波器深度Dω可以影响陷波滤波器作用频带宽窄和幅频特性下陷深度深浅；应合理设置这3个值，使陷波滤波器既能有效抑制共振频率又能对其他频率不产生影响[6]。
将陷波滤波器串入速度环输出环节如图 4所示，以整定速度环输出即电流环的给定输入，实现抑制光电云台机械共振的目的。
2.3 速度环添加自抗扰控制
将速度环控制律由比例积分（proportional integral, PI）控制器方式改为线性自抗扰控制方式（linear active disturbance rejection control, LADRC），光电云台控制原理如图 5所示。
LADRC的优势在于它将系统内外部的各种扰动和未知量统一视为一个总扰动，通过一个线性扩张状态观测器去估计该总扰动，并通过控制律实时进行补偿[7-8]。而升降式光电云台的共振扰动可视为一个未知的扰动量，可通过LADRC方式对其进行抑制。
式(2)可改写为：
$$ \left\{ {\begin{array}{*{20}{l}} {\mathop y\limits^{ \bullet \bullet \bullet } + {a_1}\mathop y\limits^{ \bullet \bullet } + {a_2}\mathop y\limits^ {\bullet} = {b_0}\mathop u\limits^ {\bullet} + {b_1}u + f} \\ {{a_1} = \frac{{({J_{\rm{M}}} + {J_{\text{L}}}{\text{)}}{f_{\rm{s}}}}}{{{J_{\rm{M}}}{J_{\text{L}}}}}\mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} } \\ {{a_{\text{2}}} = \frac{{({J_{\rm{M}}} + {J_{\text{L}}}{\text{)}}{K_{\rm{s}}}}}{{{J_{\rm{M}}}{J_{\text{L}}}}}\mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} } \\ {{b_0} = \frac{{{f_{\text{s}}}}}{{{J_{\rm{M}}}{J_{\text{L}}}}}\mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} } \\ {{b_1} = \frac{{{K_{\text{s}}}}}{{{J_{\rm{M}}}{J_{\text{L}}}}}\mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} \mathop {\mathop {}\limits^{} }\limits^{} } \end{array}} \right. $$ (5) 式中：y为电机转速ω2；u为电机转矩Te；系统f为外部扰动量。
式(5)可进一步改写为：
$$ \begin{array}{l}\stackrel{••}{y}={\displaystyle \int （{b}_{0}\stackrel{•}{u}+{b}_{1}u+f-{a}_{1}\stackrel{••}{y}-{a}_{\text{2}}\stackrel{•}{y}）\stackrel{}{}}\\ \;\; ={b}_{0}u+{\displaystyle \int ({b}_{1}u+f-{a}_{1}\stackrel{••}{y}-{a}_{\text{2}}\stackrel{•}{y})}\\ \;\; ={b}_{0}u+f{'}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\stackrel{}{}\end{array} $$ (6) 其中$f' = \int {({b_1}u + f - {a_1}\mathop y\limits^{ \bullet \bullet } - {a_{\text{2}}}\mathop y\limits^ {\bullet} )} $视为总扰动。
取x1＝ω2，${x_{\text{2}}} = \frac{{{\text{d}}{\omega _{\text{2}}}}}{{{\rm{d}}t}}$，x3＝f′，建立系统的状态方程：
$$ \left\{ {\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{{\mathop x\limits^ {\bullet} }_1}} \\ {{{\mathop x\limits^ {\bullet} }_2}} \\ {{{\mathop x\limits^ {\bullet} }_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&1 \\ 0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \\ {{x_3}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0 \\ {{b_0}} \\ 0 \end{array}} \right]u + \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ {\text{1}} \end{array}} \right]\mathop {f{{'}}}\limits^ {\bullet} } \\ {y = [\begin{array}{*{20}{c}} 0&0&1 \end{array}]\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \\ {{x_3}} \end{array}} \right]\mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} } \end{array}} \right. $$ (7) 对应可建立系统的扩张状态观测器为：
$$ \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\mathop z\limits^ {\bullet} }_1}} \\ {{{\mathop z\limits^ {\bullet} }_2}} \\ {{{\mathop z\limits^ {\bullet} }_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&1 \\ 0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{z_1}} \\ {{z_2}} \\ {{z_3}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0 \\ {\mathop {{b_0}}\limits^{\wedge} } \\ 0 \end{array}} \right]u + \left[ {\begin{array}{*{20}{c}} {{\beta _1}} \\ {{\beta _2}} \\ {{\beta _3}} \end{array}} \right]({x_1} - {z_1})} \end{array}} \right. $$ (8) 式中：z1、z2、z3分别为x1、x2、x3的观测量；$\mathop {{b_{\text{0}}}}\limits^{\wedge} $为b0的观测值。
控制律采用的比例微分控制器为：
$$ \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{u_0} = {K_{\rm{p}}}({\omega ^{\text{*}}} - \hat \omega ) + {K_{\rm{d}}}(\mathop {{\omega ^{\text{*}}}}\limits^ {\bullet} - \hat \omega )} \\ {u = \frac{{{u_0} - {f^{'}}}}{{{{\hat b}_0}}}\mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} } \end{array}} \end{array}} \right. $$ (9) 式中：ω∗为速度环给定转速；$\hat \omega $为扩展状态观测器观测到的负载转速。
3. 测试结果
光电云台方位向采用J110LWX004型无刷力矩电机和J90XFS001型双通道旋转变压器，采用的电机和旋转变压器参数见表 1。
表 1 电机和旋转变压器参数Table 1. Motor and rotary transformer parametersJ110LWX004 type motor J90XFS001 type rotary transformer Stall torque 1.5 N·m Excitation voltage 4 V Stall current 2 A Excitation frequency 2000 Hz No-load speed 240 rpm Polar number contrast 1:32 Torque coefficient 0.75 N·m/A Precision < 30″ Phase resistance 3.4 Ω Phase inductance 7.5 mH 速度环给定转速ω∗＝5°/s，测试速度环采用PI控制器和负载速度反馈采用250 Hz一阶低通滤波器时处于升起状态下光电云台方位向速度响应情况，速度环响应曲线如图 6所示。
![]()
图 6 PI+一阶250 Hz低通滤波器速度响应曲线Figure 6. PI + first-order 250 Hz low-pass filter speed response curves可见转速达到5°/s后，云台迅速进入了共振状态，已经无法正常工作。
速度环仍采用PI控制器，负载速度反馈采用二阶250 Hz巴特沃斯滤波器后，处于升起状态下光电云台方位向速度响应曲线如图 7所示。
![]()
图 7 PI+二阶250 Hz巴特沃斯滤波器速度响应曲线Figure 7. PI + second-order 250 Hz butterworth filter speed response curves可见云台方位速度环共振现象有所减弱，但云台仍处于共振状态不能正常工作。
将巴特沃斯滤波器截止频率设为60 Hz后，分别测试云台给定速度为0.5°/s、5°/s、30°/s时云台方位向速度响应曲线，如图 8所示。0.5°/s子图中小图为稳态误差段局部放大图。5°/s、30°/s子图中左侧小图为上升时间段局部放大图，右侧小图为稳态误差段局部放大图。
![]()
图 8 PI+二阶60 Hz巴特沃斯滤波器速度响应曲线Figure 8. PI + second-order 60Hz butterworth filter speed response curves可见此时云台方位向均可以正常工作，阶跃响应超调和稳态误差都较小，但较小的滤波频率会影响云台的动态性能，实际会影响云台方位向刚度。
由图 6，通过离线分析，速度环共振频率约为170 Hz，设计共振频率点为170 Hz，带宽20 Hz，深度－60 db的陷波滤波器。速度环采用PI控制器和负载速度反馈采用200 Hz一阶低通滤波器时，速度环串入该陷波滤波器后，采集处于升起状态下光电云台方位向给定速度分别为0.5°/s、5°/s、30°/s时的速度响应情况，速度环响应曲线如图 9所示。5°/s子图中左侧小图为上升时间段局部放大图，右侧小图为稳态误差段局部放大图。
可见速度环在转速较低时尚能保持正常运行，一旦转速较高受到较强激励时很容易再次发生共振。随着云台方位向的转动，云台方位向运行位置的共振频率点有所变化，使云台难以保持在其他位置也正常运行，单纯的陷波滤波器难以适应该系统的要求。也可通过在方位向多个位置进行共振频率测定方式，标注多个共振频率点，但随着桅杆长时间使用后结构上进一步松动老化，共振频率又会发生变化，难以保证光电云台系统持续运行正常。
可见云台方位向工作正常，没有发生共振现象。
分别对比给定速度为0.5°/s、5°/s、30°/s时，采用LADRC+一阶250 Hz低通滤波器方式、采用PI控制器+二阶60 Hz巴特沃斯滤波器方式、采用PI控制器+陷波滤波器方式时的速度阶跃响应曲线，对比结果如表 2所示。
表 2 不同给定转速阶跃响应情况对照表Table 2. Table of step response at different given speedGiven speed Method Rise time Adjustment time Over-shoot Steady state error 0.5°/s LADRC Fastest Fastest Minimum ±22% Butterworth filter Middle Middle Max ±30% Notch filter Slowest Slowest Middle ±32% 5°/s LADRC 53 ms 135 ms 11% ±4% Butterworth filter 77 ms 240 ms 10% ±2% Notch filter 106 ms 310 ms 9% ±6.4% 30°/s LADRC 45 ms 128 ms 8.6% ±0.7% Butterworth filter 55 ms 174 ms 7.6% ±1.2% Notch filter - - - - 由于给定速度为0.5°/s时，响应曲线稳态误差较大，因此此时仅对比响应快慢，不给出具体量化结果。由于使用陷波滤波器时，给定速度为30°/s时，系统发生共振，不给出此时的具体量化结果。
速度环采用LADRC控制器和负载速度反馈采用250 Hz一阶低通滤波器时，采集处于升起状态下光电云台方位向给定速度分别为0.5°/s、5°/s、30°/s时的速度响应情况，速度环响应曲线如图 10所示。5°/s、30°/s子图中左侧小图为上升时间段局部放大图，右侧小图为稳态误差段局部放大图。
![]()
图 10 LADRC+一阶低通滤波器速度响应曲线Figure 10. LADRC+ first-order low-pass filter speed response curves可见采用LADRC+一阶250 Hz低通滤波器方式响应速度优于其他两种方式。在稳态误差上采用LADRC+一阶250 Hz低通滤波器方式略大于采用PI控制器+二阶60 Hz巴特沃斯滤波器方式，实际中可以考虑LADRC与二阶巴特沃斯滤波器方式进行结合使用。
通过在云台方位轴心20 cm处增加一个2 kg的配重测试采用LADRC+一阶250 Hz低通滤波器方式时系统的鲁棒性，给定速度为0.5°/s、5°/s、30°/s时，增加配重前后阶跃响应对比情况如图 11所示。5°/s、30°/s子图中左侧小图为上升时间段局部放大图，右侧小图为稳态误差段局部放大图。
![]()
图 11 采用LADRC增加配重前后速度响应曲线Figure 11. Speed response curves before and after adding the counterweight used LADRC在不同的给定速度下，增加配重前后的速度阶跃响应超调有所增加，给定转速为5°/s时超调增加了5%，给定转速为30°/s时，超调增加了2.6%。调节时间和稳态误差基本一致。
通过将给定速度分别置为5°/s、10°/s、－0°/s和－5°/s，观察增加配重前后系统的动态响应情况，如图 12所示。
![]()
图 12 采用LADRC增加配重前后变速响应曲线Figure 12. Variable speed response curves before and after adding the counterweight used LADRC结合图 11、图 12综合对比，可见采用LADRC方式当系统发生结构变化也能以较好的性能正常工作，具有较好的鲁棒性。
4. 结束语
文中针对车载升降式光电云台在桅杆升起后云台方位向转动时容易共振的情况，通过对比巴特沃斯滤波器、陷波滤波器和自抗扰控制方式对云台共振的抑制效果，总结出了适用于车载升降式光电云台共振抑制的方法，可在升降式光电云台使用领域得到广泛应用。
-
[1] 陈洁, 张若岚. 应用于红外搜索跟踪和态势感知系统的全景成像技术[J]. 红外技术, 2016, 38(4): 269-279. http://hwjs.nvir.cn/article/id/hwjs201604001 CHEN Jie, ZHANG Ruolan. Panoramic imaging technology applied in IRST and status awareness system[J]. Infrared Technology, 2016, 38(4): 269-279. http://hwjs.nvir.cn/article/id/hwjs201604001
[2] 朱海滨, 邵毓, 张远健, 等. 可见光/红外双视场全景式航空侦查相机光学系统设计[J]. 应用光学, 2017, 38(1): 7-11. https://www.cnki.com.cn/Article/CJFDTOTAL-YYGX201701002.htm ZHU Haibin, SHAO Yu, ZHANG Yuanjian, et al. Optical system design of visible/infrared and double-FOV panoramic aerial camera[J]. Journal of Applied Optics, 2017, 38(1): 7-11. https://www.cnki.com.cn/Article/CJFDTOTAL-YYGX201701002.htm
[3] 贾俊涛, 唐跃峰, 毛鑫, 等. 红外全景扫描跟踪成像系统设计与实现[J]. 应用光学, 2013, 34(3): 407-412. JIA Juntao, TANG Yuefeng, MAO Xin, et al. Design and implement of infrared panoramic scanning and tracking imaging system[J]. Journal of Applied Optics, 2013, 34(3): 407-412.
[4] 李洁, 孙科峰. 机载红外搜索跟踪系统仿真测试平台设计[J]. 电光与控制, 2019, 26(8): 101-105, 110. DOI: 10.3969/j.issn.1671-637X.2019.08.019 LI Jie, SUN Kefeng. Design of a simulation testing platform for airborne IRST system[J]. Electronics Optics & Control, 2019, 26(8): 101-105, 110. DOI: 10.3969/j.issn.1671-637X.2019.08.019
[5] 何杰. 机载红外搜索跟踪系统研究与仿真实现[D]. 南京: 南京航空航天大学, 2014. HE Jie. Research and Simulation of Airborne Infrared Search and Tracking System[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014.
[6] 王辉, 周振彪, 于劲松, 等. 红外搜索跟踪系统的半实物仿真系统设计[J]. 计算机测量与控制, 2012, 20(6): 1672-1675. WANG Hui, ZHOU Zhenbiao, YU Jingsong, et al. Design of hardware-in-the-loop simulation system for infrared search and track system[J]. Computer Measurement & Control, 2012, 20(6): 1672-1675.
[7] 杨旭, 何江宁, 陈洪亮. 一种机载红外搜索跟踪系统多目标跟踪精度测试系统设计[J]. 电光与控制, 2017, 24(4): 80-84. https://www.cnki.com.cn/Article/CJFDTOTAL-DGKQ201704019.htm YANG Xu, HE Jiangning, CHEN Hongliang, et al. Design of a multi-target tracking accuracy test system for airborne IRST system[J]. Electronics Optics & Control, 2017, 24(4): 80-84. https://www.cnki.com.cn/Article/CJFDTOTAL-DGKQ201704019.htm
[8] 王卫华, 李志军, 何艳, 等. 一种基于兴趣区提取的红外搜索系统目标实时检测算法[J]. 中国激光, 2012, 39(11): 187-192. WANG Weihua, LI Zhijun, HE Yan, et al. A real-time target detection algorithm for infrared search and track system based on region of interest extraction[J]. Chinese Journal of Lasers, 2012, 39(11): 187-192.
[9] 陈炳文, 王文伟, 秦前清, 等. 基于时空融合和粒子滤波的红外弱小目标检测[J]. 红外与激光工程, 2010, 39(s): 228-232. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZYHG201005001052.htm CHEN Bingwen, WANG Wenwei, QIN Qianqing, et al. Infrared dim target detection based on space-time integration and particle filter[J]. Infrared and Laser Engineering, 2010, 39(s): 228-232. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZYHG201005001052.htm
[10] 王雪梅, 黄自力, 王德胜. 红外弱小目标的单帧捕获[J]. 红外与激光工程, 2006, 35(s): 99-104. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZYHG200611001021.htm WANG Xuemei, HUANG Zili, WANG Desheng. Infrared small and weak targets detection in single frame[J]. Infrared and Laser Engineering, 2006, 35(s): 99-104. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZYHG200611001021.htm
[11] 罗举平, 贺有, 邰新军. 基于红外图像信息的变门限检测与跟踪方法[C]//第十届全国光电技术学术交流会论文集, 2012: 243. LUO Juping, HE You, TAI Xinjun. Variable threshold detection and tracking method based on infrared image information[C]//The 10th National Conference on Optoelectronic Technology, 2012: 243.
[12] 张艳艳, 娄莉, 梁硕. 基于改进光流算法的运动目标检测技术研究[J]. 智能计算机与应用, 2018, 8(1): 55-58. DOI: 10.3969/j.issn.2095-2163.2018.01.013 ZHANG Yanyan, LOU Li, LIANG Shuo. Research on moving object detection technology based on improved optical-flow algorithm[J]. Intelligent Computer and Applications, 2018, 8(1): 55-58. DOI: 10.3969/j.issn.2095-2163.2018.01.013
[13] 西北工业大学. 一种基于连续有限帧红外图像的弱小目标检测方法: CN201911073594[P]. 中国: 2020-02-21. Northwest Polytechnic University. A method of small target detection based on continuous finite frame infrared image: CN201911073594[P]. China: 2020-02-21.
[14] WANG Lei, ZHAO Xu, LIU Yuncai. Reduce false positives for object detection by a priori probability in videos[J]. Neurocomputing, 2016, 208: 325-332. DOI: 10.1016/j.neucom.2016.03.082
[15] Recchia G, Fasano G, Accardo D, et al. An optical-flow based electro-optical see-and-avoid system for UAVs[C]//Proceedings of IEEE 2007 Aerospace Conference, 2007: DOI: 10.1109/AERO.2007.352759.
下载:
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
